（本小题满分12分。（Ⅰ）小问4分，（Ⅱ）小问8分）

如题（21）图，椭圆的中心为原点0，离心率e=，一条准线的方程是

   （Ⅰ）求该椭圆的标准方程；

   （Ⅱ）设动点P满足：，其中M、N是椭圆上的点，直线OM与ON的斜率之积为，问：是否存在定点F，使得与点P到直线l：的距离之比为定值；若存在，求F的坐标，若不存在，说明理由。

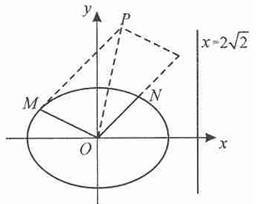
题（21）图

（本题满分12分）阅读下列材料，解决数学问题．

圆锥曲线具有非常漂亮的光学性质，被人们广泛地应用于各种设计之中，比如椭圆镜面用来制作电影放映机的聚光灯，抛物面用来制作探照灯等，它们的截面分别是椭圆和抛物线．双曲线也具有非常好的光学性质，从双曲线的一个焦点发出的光线，经过双曲线反射后，反射光线是发散的，它们好像是从另一个焦点射出的一样，如右上图所示．

反比例函数的图像是以直线为轴，以坐标轴为渐近线的等轴双曲线，记作C．

(Ⅰ)求曲线C的离心率及焦点坐标；

(Ⅱ)如右下图，从曲线C的焦点F处发出的光线经双曲线反射后得到的反射光线与入射光线垂直，求入射光线的方程．

已知曲线：（），下列叙述中正确的是         (             )

(A)  垂直于轴的直线与曲线存在两个交点                    

(B)   直线（）与曲线最多有三个交点               

(C)  曲线关于直线对称                   

(D)  若，为曲线上任意两点，则有

(本小题满分12分) 代表实数，讨论方程所表示的曲线。

（本小题满分15分）

以为焦点的椭圆过点．

(1)求椭圆C的方程；

(2)过点的动直线交椭圆于两点，试问：在坐标平面上是否存在一个定点，使得无论如何转动，以为直径的圆恒过点？若存在，求出点的坐标；若不存在，请说明理由．

（本小题12分）在平面直角坐标系中，直线与抛物线相交于．两点。

   （1）求证：“如果直线过点，那么”是真命题。

   （2）写出（1）中命题的逆命题（直线与抛物线相交于．两点为大前提），判断它是真命题还是假命题，如果是真命题，写出证明过程；如果是假命题，举出反例说明。

(本题满分12分)

已知椭圆的离心率为．斜率为的直线过椭圆的上焦点且与椭圆相交于，两点，线段的垂直平分线与轴相交于点，且当时，下焦点到直线的距离为.

（1）求椭圆的方程；

（2）求的取值范围；

（3）试用表示的面积，并求面积的最大值．

已知是椭圆的左、右焦点，过点作倾斜角为的直线交椭圆于两点，．

（1）求椭圆的离心率；

（2）若，求椭圆的标准方程．

已知是椭圆的左、右焦点，过点作倾斜角为的动直线交椭圆于两点．当时，，且．

（1）求椭圆的离心率及椭圆的标准方程；

（2）求△面积的最大值，并求出使面积达到最大值时直线的方程．

已知点P是不等式组所表示的可行域内的一动点，则点P到抛物线的焦点F的距离的最小值是         ．