（2012江苏）设为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,;当两条棱平行时,的值为两条棱之间的距离;当两条棱异面时,.

(1)求概率;

(2)求的分布列,并求其数学期望.

（2012江西理）

如图,从A1(1,0,0),A2(2,0,0),B1(0,2,0),B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点,将这3个点及原点O两两相连构成一个“立体”,记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内,此时“立体”的体积V=0).

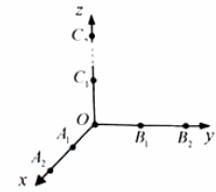
(1)求V=0的概率;

(2)求V的分布列及数学期望.

（2012辽宁理）电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图;

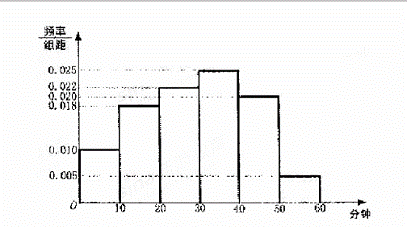
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.

(Ⅰ)根据已知条件完成下面的列联表,并据此资料你是否认为“体育迷”与性别

有关?

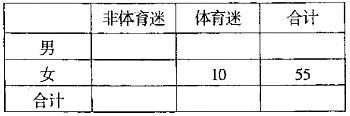
(Ⅱ)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽

样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的,求X的分布列,期望和方差.

附:

（2012山东理）先在甲、乙两个靶.某射手向甲靶射击一次,命中的概率为,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.

(Ⅰ)求该射手恰好命中一次得的概率;

(Ⅱ)求该射手的总得分的分布列及数学期望.

（2012陕西理）某银行柜台设有一个服务窗口,假设顾客办理业务所需的时间互相独立,且都是整数分钟,对以往顾客办理业务所需的时间统计结果如下:

从第一个顾客开始办理业务时计时.

(1)估计第三个顾客恰好等待4分钟开始办理业务的概率;

(2)表示至第2分钟末已办理完业务的顾客人数,求的分布列及数学期望.

（2012四川理）某居民小区有两个相互独立的安全防范系统(简称系统)和,系统和在任意时刻发生故障的概率分别为和.

(Ⅰ)若在任意时刻至少有一个系统不发生故障的概率为,求的值;

(Ⅱ)设系统在3次相互独立的检测中不发生故障的次数为随机变量,求的概率分布列及数学期望.

（2012重庆理）(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分.)

甲、乙两人轮流投篮,每人每次投一球,.约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为,乙每次投篮投中的概率为,且各次投篮互不影响.

(Ⅰ) 求甲获胜的概率;

(Ⅱ) 求投篮结束时甲的投篮次数的分布列与期望

（2012浙江理）已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和.

(Ⅰ)求X的分布列;

(Ⅱ)求X的数学期望E(X).

（2012新课标理）某花店每天以每枝元的价格从农场购进若干枝玫瑰花,然后以每枝元的价格出售,

如果当天卖不完,剩下的玫瑰花作垃圾处理.

(1)若花店一天购进枝玫瑰花,求当天的利润(单位:元)关于当天需求量

(单位:枝,)的函数解析式.

(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:

以100天记录的各需求量的频率作为各需求量发生的概率.

(i)若花店一天购进枝玫瑰花,表示当天的利润(单位:元),求的分布列,

数学期望及方差;

(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?

请说明理由.

（2012天津理）现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.

(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率:

(Ⅱ)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率:

(Ⅲ)用分别表示这4个人中去参加甲、乙游戏的人数,记,求随机变量的分布列与数学期望.