当|x|≤1时，函数f(x)＝ax＋2a＋1的值有正也有负，则实数a的取值范围是________．

命题“”的否定是                      。

已知集合，，若，则实数a的取值范围是      

已知数列的前项和为，且满足.

（1）求数列的通项公式；

（2）求证数列中不存在任意三项按原来顺序成等差数列；

（3）若从数列中依次抽取一个无限多项的等比数列，使它的所有项和满足，这样的等比数列有多少个？

设二次函数的图像过原点，，的导函数为，且，

（1）求函数，的解析式；（2）求的极小值；

（3）是否存在实常数和，使得和若存在，求出和的值；若不存在，说明理由。

某生产旅游纪念品的工厂，拟在2010年度将进行系列促销活动．经市场调查和测算，该纪念品的年销售量万件与年促销费用万元之间满足与成反比例．若不搞促销活动，纪念品的年销售量只有1万件．已知工厂2010年生产纪念品的固定投资为3万元，每生产1万件纪念品另外需要投资32万元．当工厂把每件纪念品的售价定为：“年平均每件生产成本的150%”与“年平均每件所占促销费一半”之和时，则当年的产量和销量相等．(利润=收入－生产成本－促销费用)

（1）求出与所满足的关系式；

（2）请把该工厂2010年的年利润万元表示成促销费万元的函数；

（3）试问：当2010年的促销费投入多少万元时，该工厂的年利润最大？

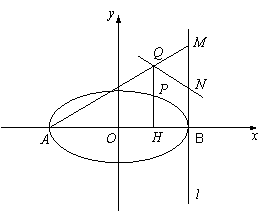
如图， 已知椭圆的长轴为，过点的直线与轴垂直．直线所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率.

（1）求椭圆的标准方程；

（2）设是椭圆上异于、的任意一点，轴，为垂足，延长到点使得，连结延长交直线于点，为的中点．试判断直线与以为直径的圆的位置关系．

在四棱锥P－ABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，PA⊥平面ABCD，E为PD的中点，PA＝2AB＝2．

（Ⅰ）求四棱锥P－ABCD的体积V；（Ⅱ）若F为PC的中点，求证PC⊥平面AEF；（Ⅲ）求证CE∥平面PAB．

已知函数

（1）若函数的图像关于点对称，且，求的值；

（2）设若的充分条件，求实数的取值范围

定义在某区间上的函数满足对该区间上的任意两个数总有不等式成立，则称函数为该区间上的上凸函数. 类比上述定义，对于数列，如果对任意正整数，总有不等式：成立，则称数列为上凸数列. 现有数列满足如下两个条件：

（1）数列为上凸数列，且；

（2）对正整数，都有，其中.

则数列中的第五项的取值范围为       .