如图，在四棱锥中，底面为直角梯形，底   面，，分别为的中点．

（1）求证：；

（2）求与平面所成的角的正弦值．

随机抽取某厂的某种产品200件，经质检，其中有一等品126件、二等品50件、三等品20件、次品4件．已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润（单位：万元）为．

（1）求的分布列；

（2）求1件产品的平均利润（即的数学期望）；

（3）经技术革新后，仍有四个等级的产品，但次品率降为，一等品率提高为．如果此时要求1件产品的平均利润不小于4.73万元，则三等品率最多是多少？

汽车是碳排放量比较大的行业之一．欧盟规定，从2012年开始，将对排放量超过

  的型新车进行惩罚．某检测单位对甲、乙两类型品牌车各抽取辆进行

  排放量检测，记录如下(单位：).

经测算发现，乙品牌车排放量的平均值为．

（1）从被检测的5辆甲类品牌车中任取2辆，则至少有一辆不符合排放量的概率是多少？

（2）若，试比较甲、乙两类品牌车排放量的稳定性．

某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名，以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎，小数点后的一位数字为叶)：

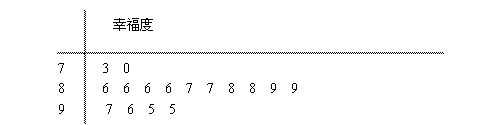
（1）指出这组数据的众数和中位数；

（2）若幸福度不低于9.5分，则称该人的幸福度为“极幸福”.求从这16人中随机选取3人，至多有1人是“极幸福”的概率；

（3）以这16人的样本数据来估计整个社区的总体数据，若从该社区(人数很多)任选3人，记表示抽到“极幸福”的人数，求的分布列及数学期望．

一缉私艇发现在方位角（从正北方向顺时针转到目标方向线的水平角）45°方向，距离15 海里的海面上有一走私船正以25 海里/小时的速度沿方位角为105°的方向逃窜．若缉私艇的速度为35 海里/小时，缉私艇沿方位角为45°+α的方向追去，若要在最短时间内追上该走私船．

（1）求角α的正弦值；

（2）求缉私艇追上走私船所需的时间．

 在中，内角所对的边长分别是, 已知，.

（1）求的值；

（2）若为的中点，求的长.

设函数.

（1）若是函数的一个零点，求的值；

（2）若是函数的一个极值点，求的值.

1.     已知函数，的最大值是1，其图像经过点

．

（1）求的解析式；

（2）已知，且，，求的值．

已知函数，设在点N*）处的切线在轴上的截距为，数列满足：N*）．

（1）求数列的通项公式；

（2）在数列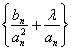中，仅当时，取最小值，求的取值范围；

（3）令函数，数列满足：，N*），

求证：对于一切的正整数，都满足：．

已知定义在上的单调函数，存在实数，使得对于任意实数，总有恒成立．

（1）求的值；

（2）若，且对任意正整数，有，

记，比较与的大小关系，并给出证明．