设复数满足，其中为虚数单位，则（    ）

A．                    B．          C．                  D．

设为等差数列的前项和，公差，若，则(     )

    A．           B．           C．               D．

若，则“”是“”的（     ）

A．充分不必要条件　        B．必要不充分条件

C．充要条件                        D．既不充分也不必要条件

设集合，则 （    ）

A．        B．    C．     D． 

已知函数f(x)=ax--2lnx

(1)若函数f(x)在其定义域内为递增函数，求实数a的取值函数；

（2）若函数f(x)的图像在x=1处的切线的斜率为0，并且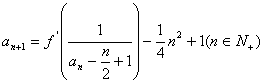.①若a₁≥3，试证明;

②若a₁=4，试比较与的大小，并说明你的理由。

已知椭圆C的中心为坐标原点O，焦点在y轴上，离心率，椭圆上的点到焦点的最短距离为, 直线l与y轴交于点P（0，m），与椭圆C交于相异两点A、B，且.（1）求椭圆方程；（2）求的取值范围．

经统计，某大型商场一个结算窗口每天排队结算的人数及相应的概率如下：

（1）    每天不超过20人排队结算的概率是多少？

（2）    一周7天中，若有3天以上（含3天）出现超过15人排队结算的概率大于0.75，商场就需要增加结算窗口。请问：该商场是否需要增加结算窗口？

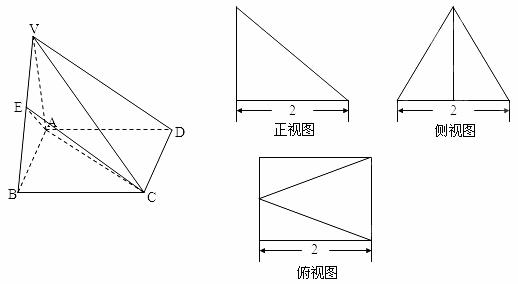
如图所示的多面体，它的正视图为直角三角形，侧视图为正三角形，俯视图为正方形（尺寸如图所示），E为VB的中点．  (1)求证：VD∥平面EAC；

(2)求二面角A—VB—D的余弦值．

如图，在某港口处获悉，其正东方向20海里处有一艘渔船遇险等待营救，此时救援船在港口的南偏西据港口10海里的处，救援船接到救援命令立即从处沿直线前往处营救渔船.

(Ⅰ) 求接到救援命令时救援船据渔船的距离；

（Ⅱ）试问救援船在处应朝北偏东多少度的方向沿直线前往处救援？（已知）.

已知数列是一个等差数列，且，.

（I）求的通项；

（II）设，,求的值。