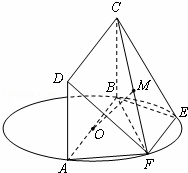
如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．

（1）求证：AF⊥平面CBF；

（2）设FC的中点为M，求证：OM∥平面DAF；

（3）设平面CBF将几何体EFABCD分成的两个锥体的体积分别为V_F﹣ABCD，V_F﹣CBE，求V_F﹣ABCD：V_F﹣CBE．

已知圆M：x²+y²﹣4x﹣8y+m=0与x轴相切．

（1）求m的值；

（2）求圆M在y轴上截得的弦长；

（3）若点P是直线3x+4y+8=0上的动点，过点P作直线PA、PB与圆M相切，A、B为切点．求四边形PAMB面积的最小值．

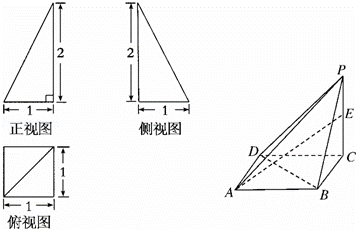
已知四棱锥P﹣ABCD的三视图和直观图如图：

（1）求四棱锥P﹣ABCD的体积；

（2）若E是侧棱PC上的动点，是否不论点E在何位置，都有BD⊥AE？证明你的结论．

（3）若F是侧棱PA上的动点，证明：不论点F在何位置，都不可能有BF⊥平面PAD．

养路处建造圆锥形仓库用于贮藏食盐（供融化高速公路上的积雪之用），已建的仓库的底面直径为12m，高4m，养路处拟建一个更大的圆锥形仓库，以存放更多食盐，现有两种方案：一是新建的仓库的底面直径比原来大4m（高不变）；二是高度增加4m（底面直径不变）

（1）分别计算按这两种方案所建的仓库的体积；

（2）分别计算按这两种方案所建的仓库的表面积；

（3）哪个方案更经济些？

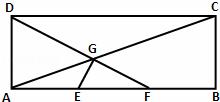
如图，在矩形ABCD中，已知AB=3，AD=1，E、F分别是AB的两个三等分点，AC，DF相交于点G，建立适当的平面直角坐标系：

（1）若动点M到D点距离等于它到C点距离的两倍，求动点M的轨迹围成区域的面积；

（2）证明：E G⊥D F．

已知三角形ABC的顶点坐标分别为A（4，1），B（1，5），C﹣3，2）；

（1）求直线AB方程的一般式；

（2）证明△ABC为直角三角形；

（3）求△ABC外接圆方程．

如图，平面中两条直线l₁和l ₂相交于点O，对于平面上任意一点M，若x，y分别是M到直线l ₁和l ₂的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：

①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；

②若pq=0，且p+q≠0，则“距离坐标”为（ p，q） 的点有且只有2个；

③若pq≠0则“距离坐标”为 （ p，q） 的点有且只有3个．

上述命题中，正确的有　①②　．（填上所有正确结论对应的序号）

已知母线长为6，底面半径为3的圆锥内有一球，球与圆锥的底面及圆锥的所有母线都相切，则球的体积　．

在正方体ABCD﹣A₁B₁C₁D₁中，M和N分别为BC、C₁C的中点，那么异面直线MN与AC所成的角等于　　．

空间直角坐标系中，已知A（1，0，2），B（1，﹣3，1），点P在z轴上，且|PA|=|PB|，则点P的坐标为　　．