
科目: 来源: 题型:
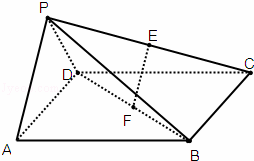
如图在四棱锥P﹣ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=![]() AD,设E、F分别为PC、BD的中点.
AD,设E、F分别为PC、BD的中点.
(Ⅰ) 求证:EF∥平面PAD;
(Ⅱ) 求证:面PAB⊥平面PDC;
(Ⅲ) 求二面角B﹣PD﹣C的正切值.
查看答案和解析>>
科目: 来源: 题型:
甲、乙两人参加某种选拔测试.规定每人必须从备选的6道题中随机抽出3道题进行测试,在备选的6道题中,甲答对其中每道题的概率都是![]() ,乙只能答对其中的3道题.答对一题加10分,答错一题(不答视为答错)得0分.
,乙只能答对其中的3道题.答对一题加10分,答错一题(不答视为答错)得0分.
(Ⅰ)求乙得分的分布列和数学期望;
(Ⅱ)规定:每个人至少得20分才能通过测试,求甲、乙两人中至少有一人通过测试的概率.
查看答案和解析>>
科目: 来源: 题型:
已知函数f(x)=sin2x+2![]() sinxcosx+3cos2x,x∈R.求:
sinxcosx+3cos2x,x∈R.求:
(I)求函数f(x)的最小正周期和单调递增区间;
(II)求函数f(x)在区间![]() 上的值域.
上的值域.
查看答案和解析>>
科目: 来源: 题型:
设函数![]() ,A0为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量
,A0为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量![]() ,向量i=(1,0),设θn为向量an与向量i的夹角,则满足
,向量i=(1,0),设θn为向量an与向量i的夹角,则满足![]() 的最大整数n是 .
的最大整数n是 .
查看答案和解析>>
科目: 来源: 题型:
某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为2:3:4,现用分层抽样方法抽出一个容量为n的样本,其中A型号产品有16件,那么此样品容量为n= .
查看答案和解析>>
科目: 来源: 题型:
已知函数f(x)=1+x﹣![]() +
+![]() ﹣
﹣![]() +…+
+…+![]() ,g(x)=1﹣x+
,g(x)=1﹣x+![]() ﹣
﹣![]() +
+![]() ﹣…﹣
﹣…﹣![]() ,设函数F(x)=f(x+3)•g(x﹣4),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z内,则b﹣a的最小值为( )
,设函数F(x)=f(x+3)•g(x﹣4),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z内,则b﹣a的最小值为( )
|
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com