
科目: 来源: 题型:
若a、b、c是△ABC的三边,直线ax+by+c=0与圆x2+y2=1相离,则△ABC一定是( )
(A)直角三角形 (B)等边三角形
(C)锐角三角形 (D)钝角三角形
查看答案和解析>>
科目: 来源: 题型:
曲线y=2sin(x+![]() )cos(x-
)cos(x-![]() )与直线y=
)与直线y=![]() 在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3、…,则|P2P4|等于( )
在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3、…,则|P2P4|等于( )
(A)![]() (B)2
(B)2![]() (C)3
(C)3![]() (D)4
(D)4![]()
查看答案和解析>>
科目: 来源: 题型:
由下列条件解△ABC,其中有两解的是( )
(A)b=20,A=45°,C=80° (B)a=30,c=28,B=60°
(C)a=14,c=16,A=45° (D)a=12,c=15,A=120°
查看答案和解析>>
科目: 来源: 题型:
已知函数y=cos(ωx+φ)(ω>0,|φ|<![]() )的部分图象如图所示,则( )
)的部分图象如图所示,则( )
(A)ω=1,φ=![]() (B)ω=1,φ=-
(B)ω=1,φ=-![]() (C)ω=2,φ=
(C)ω=2,φ=![]() (D)ω=2,φ=-
(D)ω=2,φ=-![]()
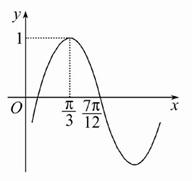
查看答案和解析>>
科目: 来源: 题型:
下列说法正确的是( )
(A)第二象限的角比第一象限的角大
(B)若sinα=![]() ,则α=
,则α=![]()
(C)三角形的内角是第一象限角或第二象限![]() 角
角
(D)不论用角度制还是弧度制度量一个角,它们与扇形所对应的半径的大小无关
查看答案和解析>>
科目: 来源: 题型:
已知函数f(x)的导数f′(x)=3x2-3ax,f(![]() 0)=b,a,b为实数,1<a<2.
0)=b,a,b为实数,1<a<2.
(1)若f(x)在区间[-1,1]上的最小值、最大值分别为-2、1,求a、b的值;
(2)在(1)的条件下,求经过点P(2,1)且与曲线f(x)相切的直线l的方程;
(3)设函数F(x)=[f′(x)+6x+1]·e2x,试判断函数F(x)的极值点个数.
查看答案和解析>>
科目: 来源: 题型:
设函数f(x)=(x+a)·lnx-x+a.
(1)设g(x)=f′(x),求函数g(x)的单调区间;
(2)若a≥![]() ,试研究函数f(x)=(x+a)lnx-x+a的零点个数.
,试研究函数f(x)=(x+a)lnx-x+a的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com