
科目: 来源: 题型:
选修4——4;坐标系与参数方程
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线
![]() ,过点P(-2,-4)的直线
,过点P(-2,-4)的直线 为参数)与曲线C相交于点M,N两点.
为参数)与曲线C相交于点M,N两点.
(Ⅰ)求曲线C和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若|PM|,|MN|,|PN |成等比数列,求实数a的值
查看答案和解析>>
科目: 来源: 题型:
选修4-1几何证明选讲
如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。
(Ⅰ)若![]() ,求CD的长;
,求CD的长;
(Ⅱ)若 ∠ADO :∠EDO=4 :1,求扇形OAC(阴影部分)的面积(结果保留![]() )。
)。
 |
查看答案和解析>>
科目: 来源: 题型:
已知函数![]() (
(![]() ).(Ⅰ)当
).(Ⅰ)当![]() 时,求
时,求![]() 的图象在
的图象在![]() 处的切线方程;(Ⅱ)若函数
处的切线方程;(Ⅱ)若函数![]() 在
在![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若函数![]() 的图象与
的图象与![]() 轴有两个不同的交点
轴有两个不同的交点![]() ,且
,且![]() ,
,
求证:![]() (其中
(其中![]() 是
是![]() 的导函数).
的导函数).
查看答案和解析>>
科目: 来源: 题型:
已知点M是椭圆C:![]() =1(a>b>0)上一点,F1、F2分别为C的左、右焦点,|F1F2|=4,
=1(a>b>0)上一点,F1、F2分别为C的左、右焦点,|F1F2|=4,
∠F1MF2 =60o,![]() F1 MF2的面积为
F1 MF2的面积为![]() (I)求椭圆C的方程; ( II)设N(0,2),过点
(I)求椭圆C的方程; ( II)设N(0,2),过点
p(-1,-2)作直线l,交椭圆C异于N的A、B两点,直线NA、NB的斜率分别为k1、k2,证明:k1+k2为定值.
查看答案和解析>>
科目: 来源: 题型:
某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究,对该校高二年级800
名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有
60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人。
(Ⅰ)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?
(Ⅱ)将上述调查所得到的频率视为概率,从该校高二年纪学生成绩中,有放回地随机抽
取3名学生的成绩,记抽取的3个成绩中语文、外语两科成绩至少有一科优秀的个数为X,
求X的分布列和期望![]() 。
。
|
| 0.010 | 0.005 | 0.001 |
|
| 6.635 | 7.879 | 10.828 |
附:![]()
查看答案和解析>>
科目: 来源: 题型:
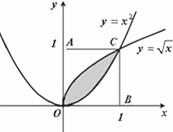
如图所示,在一个边长为1的正方形AOBC内,曲y=x2和曲线y=![]() 围成一个叶形图(阴影部分),向正方形AOBC内随机投一点(该点落在正方形AOBC内任何一点是等可能的),则所投的点落在叶形图内部的概率是 .
围成一个叶形图(阴影部分),向正方形AOBC内随机投一点(该点落在正方形AOBC内任何一点是等可能的),则所投的点落在叶形图内部的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com