
科目: 来源: 题型:
下面四个图案,都是由小正三角形构成,设第n个图形中所有![]() 小正三角形边上黑点的总数为
小正三角形边上黑点的总数为![]() .
.




图1 图2 图3 图4
(1)求出![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)找出![]() 与
与![]() 的关系,并求出
的关系,并求出![]() 的表达式;
的表达式;
(3)求证: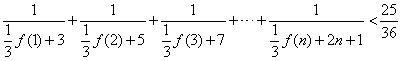 (
(![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
在对某校高一学生体育选修项目的一次调查中,共调查了160人,其中女生85人,男生75人.女生中有60人选修排球,其余的人选修篮球;男生中有20人选修排球,其余的人选修篮球.(每人必须选一项,且只能选一项)
(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.001的前提下认为性别与体育选修项目有关?
参考公式及数据:![]() ,其中
,其中![]() .
.
| K2≥k0 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,x轴的正半轴为极轴建立极坐标系,圆
为极点,x轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将圆![]() 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)圆![]() 、
、![]() 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
已知函数![]() 和点
和点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() .
.
(Ⅰ)设![]() ,试求函数
,试求函数![]() 的表达式;
的表达式;
(Ⅱ)是否存在![]() ,使得
,使得![]() 、
、![]() 与
与![]() 三点共线.若存在,求出
三点共线.若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数![]() ,在区间
,在区间![]() 内总存在
内总存在![]() 个实数
个实数![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,求
成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
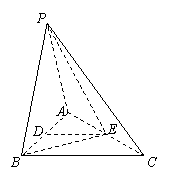

(1)求证:DE∥平面PBC;
(2)求证:AB⊥PE;
(3)求二面角A-PB-E的大小.
查看答案和解析>>
科目: 来源: 题型:
电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则是:一个方块下面有一个雷或没有雷,如果无雷,掀开方块下面就会标有数字(如果数字是0,常省略不标),此数字表明它周围的方块中雷的个数(至多八个),如图甲中的“3”表示它的周围八个方块中有且仅有3个雷.图乙是张三玩的游戏中的局部,根据图乙中信息,上方第一行左起七个方块中(方块上标有字母),能够确定下面一定没有雷的方块有 ,下面一定有雷的方块有 .(请填入所有选定方块上的字母)
查看答案和解析>>
科目: 来源: 题型:
设集合![]() ,如果
,如果![]() 满足:对任意
满足:对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() ,那么称
,那么称![]() 为集合
为集合![]() 的一个聚点,则在下列集合中:(1)
的一个聚点,则在下列集合中:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() ,以
,以![]() 为聚点的集合有 .
为聚点的集合有 .
(写出所有你认为正确的结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com