
科目: 来源: 题型:
已知函数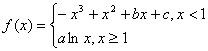 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点![]() 处的切线的斜率是
处的切线的斜率是![]() .
.
(Ⅰ)求实数![]() 的值; (Ⅱ)求
的值; (Ⅱ)求![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数![]() ,曲线
,曲线![]() 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得![]() 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在![]() 轴上?说明理由.
轴上?说明理由.
查看答案和解析>>
科目: 来源: 题型:
| |
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() (4,0)且不与坐标轴垂直的直线
(4,0)且不与坐标轴垂直的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,设点
两点,设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(ⅰ)求证:直线![]() 过
过![]() 轴上一定点,并求出此定点坐标;
轴上一定点,并求出此定点坐标;
(ⅱ)求△![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
如图,已知![]() 为平行四边形,
为平行四边形,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() 与
与![]() 相交于
相交于![]() .现将四边形
.现将四边形![]() 沿
沿![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 上的射影恰在直线
上的射影恰在直线![]() 上.
上.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
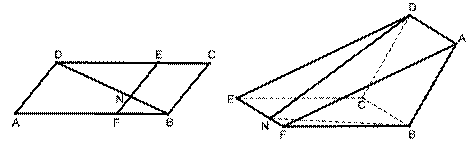 (Ⅱ)求折后直线DN与直线BF所成角的余弦值;
(Ⅱ)求折后直线DN与直线BF所成角的余弦值;
(Ⅲ)求三棱锥N—ABF的体积.
查看答案和解析>>
科目: 来源: 题型:
某水泥厂甲、乙两个车间包装水泥,在自动包装传送带上每隔30分钟抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102,101,99,98,103,98,99
乙:110,115,90,85,75,115,110
(1)画出这两组数据的茎叶图;
(2)求出这两组数据的平均值和方差(用分数表示);并说明哪个车间的产品较稳定.
(3)从甲中任取一个数据x(x≥100),从乙中任取一个数据y(y≤100),求满足条件|x-y|≤20的概率.
查看答案和解析>>
科目: 来源: 题型:
某兴趣小组测量电视塔AE的高度H(单位m),如示意图,垂直放置的标杆BC高度h=4m,仰角∠ABE=α,∠ADE=β
(1)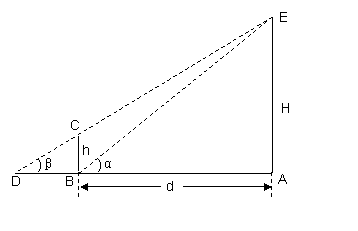 该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20,,请据此算出H的值
该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20,,请据此算出H的值
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位m),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125m,问d为多少时,α-β最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com