下列说法正确的是                                                  （    ）                                                                                                                

A. 命题“使得 ”的否定是：“”

B. “”是“在上为增函数”的充要条件

C. “为真命题”是“为真命题”的必要不充分条件

D. 命题p：“”，则p是真命题

已知复数z满足为虚数单位），则复数所对应的点所在象限为 （    ）

A．第一象限      B． 第二象限    C．第三象限      D．第四象限

设集合，则等于                  （    ）

A.      B.      C.     D.

已知函数f(x)= |x-1|,g(x)= - |x+3| + a (aÎR)

解关于的不等式；

（2）若函数的图像恒在函数的图像的上方，求实数的取值范围.

以直角坐标系的原点为极点，轴的正半轴为极轴，且两个坐标系取相等的长度单位．已知直线的参数方程为 (为参数，)，曲线的极坐标方程为．

（Ⅰ）求曲线的直角坐标方程；

（Ⅱ ）设直线与曲线相交于、两点，当变化时，求的最小值．

在中，AB=AC，过点A的直线与其外接圆交于点P，交BC延长线于点D。

（1）求证： ；（2）若AC=3，求的值。

已知函数.

（Ⅰ）求函数的单调区间；

（Ⅱ）若函数上是减函数，求实数a的最小值；

（Ⅲ）若，使（）成立，求实数a的取值范围.

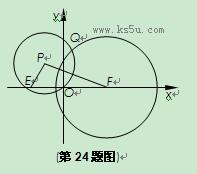
如图，已知O (0，0)，E(－，0)，F(，0)，圆F：(x－)²＋y²＝5．动点P满足|PE|＋|PF|＝4．以P为圆心，|OP|为半径的圆P与圆F的一个公共点为Q．

(Ⅰ) 求点P的轨迹方程；(Ⅱ) 求点Q到直线PF的距离

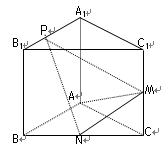
如图，已知三棱柱ABC－A₁B₁C₁的侧棱与底面垂直，AA₁＝AB＝AC＝1，AB⊥AC，M、N分别是CC₁，BC的中点，点P在直线A₁B₁上，且

（1）证明：无论入取何值，总有AM⊥PN；

（2）当入取何值时，直线PN与平面ABC所成的角θ最大？并求该角取最大值时的正切值。

（3）是否存在点P，使得平面PMN与平面ABC所成的二面角为30º，若存在，试确定点P的位置，若不存在，说明理由。

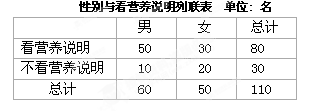
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表：

（1）从这50名女生中按是否看营养说明采取分层抽样，抽取一个容量为的样本，问样本中看与不看营养说明的女生各有多少名?

(2) 从（1）中的5名女生样本中随机选取两名作深度访谈, 求选到看与不看营养说明的女生各一名的概率；

（3）根据以上列联表，问有多大把握认为“性别与在购买食物时看营养说明”有关？