已知m,n是不重合的直线,a,b分别垂直于两个不重合的平面α,β,有以下四个命题:

①若m⊥a,n∥b,且α⊥β,则m∥n.

②若m∥a,n∥b且α⊥β,则m⊥n.

③若m∥a,n⊥b且α∥β,则m⊥n.

④若m⊥a,n⊥b且α⊥β,则m∥n.

其中真命题的序号是　　　　.

如图,在正方体ABCD-A₁B₁C₁D₁中,M,N分别是棱C₁D₁,C₁C的中点.以下四个结论:

①直线AM与直线CC₁相交;

②直线AM与直线BN平行;

③直线AM与直线DD₁异面;

④直线BN与直线MB₁异面.

其中正确结论的序号为　　　    (注:把你认为正确的结论序号都填上).

如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=(　　)

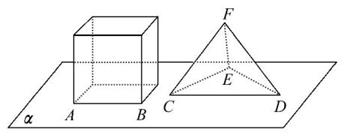
A.8         B.9     C.10            D.11

设l为直线,α,β是两个不同的平面,下列命题中正确的是(　　)

A.若l∥α,l∥β,则α∥β

B.若l⊥α,l⊥β,则α∥β

C.若l⊥α,l∥β,则α∥β

D.若α⊥β,l∥α,则l⊥β

已知m,n,l是三条不同的直线,α,β,γ是三个不同的平面,给出以下命题:

①若m⊂α,n∥α,则m∥n;②若m⊂α,n⊂β,α⊥β,α∩β=l,m⊥l,则m⊥n;③若n∥m,m⊂α,则n∥α;④若α∥γ,β∥γ,则α∥β.其中正确命题的序号是(　　)

A.②④              B.②③

C.③④              D.①③

已知l,m是两条不同的直线,α,β是两个不同的平面,有下列五个命题:

①若l⊂β,且α∥β,则l∥α;

②若l⊥β,且α∥β,则l⊥α;

③若l⊥β,且α⊥β,则l∥α;

④α∩β=m,且l∥m,则l∥α;

⑤若α∩β=m,l∥α,l∥β,则l∥m.则所有正确命题的序号是(　　)

A.①③⑤                    B.②④⑤

C.①②⑤                    D.①②④

设a,b是不同的直线,α,β是不同的平面,则下列命题:

①若a⊥b,a∥α,则b∥α　   ②若a∥α,α⊥β,则a⊥β

③若a⊥β,α⊥β,则a∥α　④若a⊥b,a⊥α,b⊥β,则α⊥β

其中正确命题的个数是(　　)

A.0　　　   B.1　　 　C.2　　　 D.3

已知S_n是等比数列{a_n}的前n项和,S₄,S₂,S₃成等差数列,且a₂+a₃+a₄=-18.

(1)求数列{a_n}的通项公式.

(2)是否存在正整数n,使得S_n≥2 013?若存在,求出符合条件的所有n的集合;若不存在,说明理由.

设数列{a_n}的前n项和S_n=n²,数列{b_n}满足b_n=(m∈N^*).

(1)若b₁,b₂,b₈成等比数列,试求m的值.

(2)是否存在m,使得数列{b_n}中存在某项b_t满足b₁,b₄,b_t(t∈N^*,t≥5)成等差数列?若存在,请指出符合题意的m的个数;若不存在,请说明理由.

已知数列{a_n}的前n项和为S_n,a₁=t,2a_n+1=-3S_n+4(n∈N^*)

(1)当t为何值时,数列{a_n}是等比数列?

(2)在(1)的条件下,设b_n=λa_n-n²,若数列{b_n}中有b₁>b₂,b₃>b₄,…,b_2n-1>b_2n…成立,求实数λ的取值范围.