
科目: 来源: 题型:
通过随机询问100名性别不同的大学生是否![]() 爱好踢毽子运动,得到如下的列联表:
爱好踢毽子运动,得到如下的列联表:
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好] | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
附表:
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
随机变量K2=![]() ,经计算,统计量K2的观测值k≈4.762,参照附表,得到的正确结论是( )
,经计算,统计量K2的观测值k≈4.762,参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.05的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.05的前提下,认为“爱好该项运动与性别![]() 无关”
无关”
C.在犯错误的概率不超过0.025的前提下认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.025的前提下认为“爱好该项运动与性别无关”
查看答案和解析>>
科目: 来源: 题型:
已知某中学高三(1)班某同学从高二以来每次数学考试成绩的茎叶图如图所示,则该同学考试成绩的中位数、众数、极差分别为 ( )

A.118,118,36 B.111,118,131
C.125,111,118 D.111,118,36
查看答案和解析>>
科目: 来源: 题型:
已知x,y的取值如下表:
| x | 0 | 1 | 4 | 5 | 6 | 8 |
| y | 1.3 | 1.8 | 5.6 | 6.1 | 7.4 | 9.3 |
从所得的散点图分析可知:y与x线性相关,且![]() =0.95x+
=0.95x+![]() ,则
,则![]() =( )
=( )
A.1.30 B.1.45 C.1.65 D.1.80
查看答案和解析>>
科目: 来源: 题型:
交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查.假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为( )
A.101 B.808
C.1 212 D.![]() 2 012
2 012
查看答案和解析>>
科目: 来源: 题型:
正项等比数列{an}的前n项和为Sn,a4=16,且a2,a3的等差中项为S2.
(1)求数列{an}的通项公式.
(2)设bn=![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目: 来源: 题型:
设数列{an}的前n项和为Sn,点(an,Sn)在直线y=![]() x-1上.
x-1上.
(1)求数列{an}的通项公式.
(2)在an与an+1之间插入n个数,使这n+2个数组成公差为dn的等差数列,求数列![]() 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
科目: 来源: 题型:
设数列{an}满足:a1=1,an+1=3an,n∈N+.
(1)求{an}的通项公式及前n项和Sn.
(2)已知{bn}是等差数列,Tn为前n项和,且b1=a2,b3=a1+a2+a3,求T20.
查看答案和解析>>
科目: 来源: 题型:
若数列{an}满足:存在正整数T,对于任意正整数n都有an+T=an成立,则称数列{an}为周期数列,周期为T,已知数列{an![]() }满足a1=m(m>0),an+1=
}满足a1=m(m>0),an+1=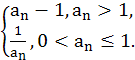 则下列结论正确的有 .
则下列结论正确的有 .
①若m=![]() ,则a5=3;②若a3=
,则a5=3;②若a3=![]() 2,则m可以取3个不同的值;③若m=
2,则m可以取3个不同的值;③若m=![]() ,则数列{an}是周期为3的数列;④∃m∈Q且m≥2,数列{an}是周期数列.
,则数列{an}是周期为3的数列;④∃m∈Q且m≥2,数列{an}是周期数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com