
科目: 来源:2012届河南省郑州盛同学校高三上学期第一次月考文科数学 题型:解答题
(本小题满分16分)
定义在D上的函数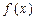 ,如果满足:对任意
,如果满足:对任意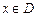 ,存在常数
,存在常数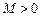 ,都有
,都有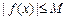 成立,则称
成立,则称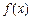 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数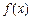 的上界.
的上界.
已知函数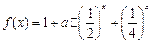 ;
;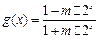 .
.
(1)当a=1时,求函数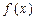 在
在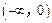 上的值域,并判断函数
上的值域,并判断函数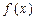 在
在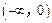 上是否为有界数,请说明理由;
上是否为有界数,请说明理由;
(2)若函数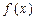 在
在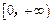 上是以3为上界的
上是以3为上界的 有界函数,求实数a的取值范围;
有界函数,求实数a的取值范围;
(3)若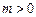 ,函
,函 数
数 在
在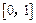 上的上界是
上的上界是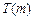 ,求
,求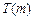 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2012届河南省郑州盛同学校高三上学期第一次月考文科数学 题型:解答题
(本小题满分14分)
已知函数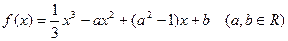 .
.
(1)若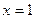 为
为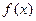 的极值点,求
的极值点,求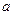 的值;
的值;
(2)若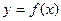 的图象在点(
的图象在点(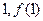 )处的切线方程为
)处的切线方程为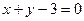 ,
,
( 3 )求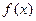 在区间
在区间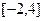 上的最大值;
上的最大值;
(4)求函数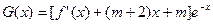 (
(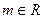 )的单调区间.
)的单调区间.
查看答案和解析>>
科目: 来源:2010-2011年陕西省汉中市汉台区高二下学期期末文科数学 题型:解答题
(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。(Ⅰ)将总费用y表示为x的函数
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用
查看答案和解析>>
科目: 来源:2012届广东省情缘盛兴中英文学校高三第一学期8月月考文科数学 题型:解答题
(本小题满分14分)
在矩形ABCD中,已知 ,在AB、AD、CD、CB上分别
,在AB、AD、CD、CB上分别
截取AE、AH、CG、CF都等于 ,
,
(1)将四边形EFGH的面积S表示成 的函数,并写出函数的定义域
的函数,并写出函数的定义域
(2)当 为何值时,四边形EFGH的面积最大?并求出最大面积
为何值时,四边形EFGH的面积最大?并求出最大面积
查看答案和解析>>
科目: 来源:2012届安徽省桐城八中高三年级模拟测试数学(一) 题型:解答题
(本小题满分12分)
已知函数f(x)= (1+x)2-ln(1+x),
(1+x)2-ln(1+x),
(1)求f(x)的单调区间;(2)若x∈ 时,f(x)<m恒成立,求m的取值范围.?
时,f(x)<m恒成立,求m的取值范围.?
查看答案和解析>>
科目: 来源:2012届安徽省泗县双语中学高三摸底考试理科数学 题型:解答题
附加题(本大题共两个小题,每个小题10分,满分 20分,省级示范性高中要
把该题成绩计入总分,普通高中学生选作)
已知 ,
,
(1)判断函数在区间(-∞,0)上的单调性,并用定义证明;
(2)画出该函数在定义域上的图像.(图像体现出函数性质即可)
查看答案和解析>>
科目: 来源:2012届福建省邵武四中高三年级八月份月考试卷理科数学 题型:解答题
(本小题满分13分)已知定义域为 的函数
的函数 是奇函数.
是奇函数.
(1)求 的值;(2)判断函数
的值;(2)判断函数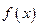 的单调性;
的单调性;
(3)若对任意的 ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目: 来源:2010-2011学年北京师大附中高二下学期期中考试文科数学 题型:解答题
已知函数 ,
, ,设
,设 。
。
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若以函数 图像上任意一点
图像上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数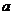 的最小值。
的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com