
科目: 来源:2010年扬州中学高一下学期期末考试数学 题型:解答题
(本小题满分16分) 一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).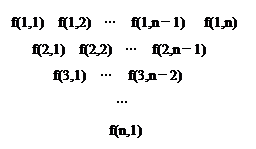
(1)若数表中第i (1≤i≤n-3)行的数依次成等差数列,求证:第i+1行的数也依次成等差数列;
(2)已知f(1,j)=4j,求f(i,1)关于i的表达式;
(3)在(2)的条件下,若f(i,1)=(i+1)(ai-1),bi= ,试求一个函数g(x),使得
Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当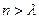 时,都有Sn >m.
时,都有Sn >m.
查看答案和解析>>
科目: 来源:2010年广东省高考冲刺强化训练试卷八文科数学 题型:解答题
(本小题满分14分)已知公差大于零的等差数列{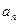 }的前n项和为
}的前n项和为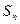 ,且满足
,且满足 ,
,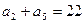 .
. ⑴求通项
⑴求通项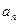 ;
;
⑵若数列
 是等差数列,且
是等差数列,且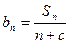 ,求非零常数c;
,求非零常数c;
⑶比较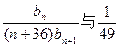 (
(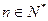 )的大小.
)的大小.
查看答案和解析>>
科目: 来源:福建省三明一中2009-2010下学期学段考试卷高一数学试题 题型:解答题
本小题11分
已知数列 是等差数列,
是等差数列, 11且,
11且, 是数列
是数列 的前
的前 项和。
项和。
(1)求数列 的通项公式
的通项公式 及前
及前 项和
项和 。 K^S*5U.C
。 K^S*5U.C
(2)设正项等比数列 满足
满足 ,
, ,数列
,数列 的通项公式
的通项公式
(3)在(2)的条件下若 ,求
,求 的值。 K^S*5U.C
的值。 K^S*5U.C
查看答案和解析>>
科目: 来源:2009—2010学年广州市七区联考高二数学(理)下学期期末监测 题型:解答题
(本小题满分14分)
设等差数列 前
前 项和为
项和为 ,则有以下性质:
,则有以下性质: 成等差数列.
成等差数列.
(1) 类比等差数列的上述性质,写出等比数列 前
前 项积
项积 的类似性质;
的类似性质;
(2) 证明(1)中所得结论.
查看答案和解析>>
科目: 来源:2009-2010学年邯郸市高一第二学期期末教学质量检测 题型:解答题
(普通高中做)
已知等差数列 中,
中, 为
为 的前
的前 项和,
项和, .
.
(Ⅰ)求 的通项
的通项 与
与 ;
;
(Ⅱ)当 为何值时,
为何值时, 为最大?最大值为多少?
为最大?最大值为多少?
查看答案和解析>>
科目: 来源:湖北省黄冈中学2010年春季高一 数学期中考试试题(理) 题型:解答题
(本题满分12分)成等差数列的三个数的和等于 ,并且这三个数分别加上
,并且这三个数分别加上 ,
, ,
, 后就成了等比数列,求这三个数排成的等差数列.
后就成了等比数列,求这三个数排成的等差数列.
查看答案和解析>>
科目: 来源:河北省衡水中学2009-2010学年度第二学期二调考试高一年级数学试卷理科 题型:解答题
(本小题共12分)已知数列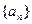 的前n项和
的前n项和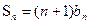 ,其中
,其中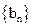 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列,
(1)求数列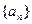 的通项公式;高@考☆资&源*网
的通项公式;高@考☆资&源*网
(2)若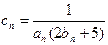 ,求数列
,求数列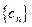 的前n项和
的前n项和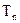
查看答案和解析>>
科目: 来源:2010年高考试题分项版文科数学之专题三 数列 题型:解答题
(本小题满分12分)
已知{an}是公差不为零的等差数列,a1=1,且a1,a3,a9成等比数列.
(Ⅰ)求数列{an}的通项; (Ⅱ)求数列 的前n项和Sn.
的前n项和Sn.
查看答案和解析>>
科目: 来源:2010年高考试题分项版文科数学之专题十五 推理与证明 题型:解答题
正实数数列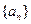 中,
中,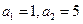 ,且
,且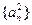 成等差数列.
成等差数列.
(1) 证明数列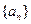 中有无穷多项为无理数;
中有无穷多项为无理数;
(2)当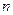 为何值时,
为何值时,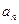 为整数,并求出使
为整数,并求出使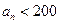 的所有整数项的和.
的所有整数项的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com