（本小题满分14分）（注意：在试题卷上作答无效）
设数列的前项和为，对一切，点都在函数 的图象上．
(Ⅰ)求及数列的通项公式；
(Ⅱ) 将数列依次按1项、2项、3项、4项循环地分为（），（，），（，，），（，，，）；（），（，），(，，），（，，，）；（），…，分别计算各个括号内各数之和，设由这些和按原来括号的前后顺序构成的数列为，求的值；
（Ⅲ）令（），求证：

（本小题满分12分）设为数列的前项和，，，其中是常数．
（1）求及；
（2）若对于任意的，，，成等比数列，求的值．

（本小题满分10分）
已知数列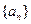的通项公式为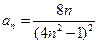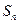，为其前项的和．计算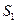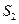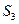，，的值，根据计算结果，推测出计算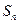的公式，并用数学归纳法加以证明．

（本小题满分12分）
是首项的等比数列，其前项和为S_n，且成等比数列．
（1）求数列的通项公式；
（2）若，设为数列的前项和，
求证：

（本小题满分12 分）
已知{ }是整数组成的数列，a₁ = 1，且点在函数的图象上，
（1）求数列{}的通项公式；
（2）若数列{}满足 = 1，，求证：

设数列
（1）求

（本小题满分10分）
小正方形按照如图规律排列，用表示图（n）中小正方形的个数（n为正整数）。
（I）按照如图规律写出的值；
（II）合情推理写出的表达式，并简要写出推理过程。

（满分10分）已知数列,,若以为系数的二次方程都有根，且满足。
（1）求数列通项公式；
（2）求数列前项和．

(本小题共13分)
已知数列的前项和为,且.
数列满足()，且，.
（Ⅰ）求数列，的通项公式；
（Ⅱ）设，数列的前项和为，求使不等式对一切都成立的最大正整数的值；
（Ⅲ）设是否存在，使得 成立？若存在，求出的值；若不存在，请说明理由．

（14分）
设集合W由满足下列两个条件的数列构成：
①
②存在实数M，使（n为正整数）
（I）在只有5项的有限数列
；试判断数列是否为集合W的元素；
（II）设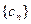是等差数列，是其前n项和，证明数列；并写出M的取值范围；
（III）设数列且对满足条件的常数M，存在正整数k，使
求证：