
科目: 来源:2007年普通高等学校招生全国统一考试理科数学卷(浙江) 题型:解答题
(本题15分)已知数列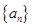 中的相邻两项
中的相邻两项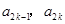 是关于
是关于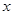 的方程
的方程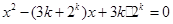 的两个根,且
的两个根,且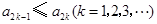 .
.
(I)求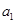 ,
,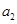 ,
,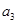 ,
,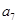 ;
;
(II)求数列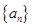 的前
的前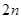 项和
项和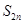 ;
;
(Ⅲ)记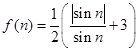 ,
,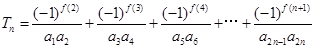 ,求证:
,求证: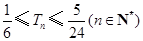 .
.
查看答案和解析>>
科目: 来源:2007年普通高等学校招生全国统一考试理科数学卷(重庆) 题型:解答题
(本小题满分12分)已知各项均为正数的数列{ }的前n项和满足
}的前n项和满足 ,且
,且
(1)求{ }的通项公式;(5分)
}的通项公式;(5分)
(2)设数列{ }满足
}满足 ,并记
,并记 为{
为{ }的前n项和,求证:
}的前n项和,求证: . (7分)
. (7分)
查看答案和解析>>
科目: 来源:2007年普通高等学校招生全国统一考试理科数学卷(上海) 题型:解答题
若有穷数列 (
( 是正整数),满足
是正整数),满足 即
即
( 是正整数,且
是正整数,且 ),就称该数列为“对称数列”。
),就称该数列为“对称数列”。
(1)已知数列 是项数为7的对称数列,且
是项数为7的对称数列,且 成等差数列,
成等差数列, ,试写出
,试写出 的每一项
的每一项
(2)已知 是项数为
是项数为 的对称数列,且
的对称数列,且 构成首项为50,公差为
构成首项为50,公差为 的等差数列,数列
的等差数列,数列 的前
的前 项和为
项和为 ,则当
,则当 为何值时,
为何值时, 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数 ,试写出所有项数不超过
,试写出所有项数不超过 的对称数列,使得
的对称数列,使得 成为数列中的连续项;当
成为数列中的连续项;当 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和
查看答案和解析>>
科目: 来源:2007年普通高等学校招生全国统一考试理科数学卷(陕西) 题型:解答题
(本小题满分12分)
已知各项全不为零的数列{ak}的前k项和为Sk,且Sk= N*),其中a1=1.
N*),其中a1=1.
(Ⅰ)求数列{ak}的通项公式;
(Ⅱ)对任意给定的正整数n(n≥2),数列{bk}满足 (k=1,2,…,n-1),b1=1.
(k=1,2,…,n-1),b1=1.
求b1+b2+…+bn.
查看答案和解析>>
科目: 来源:2007年普通高等学校招生全国统一考试理科数学卷(辽宁) 题型:解答题
(本小题满分12分)已知数列 ,
, 与函数
与函数 ,
, ,
, 满足条件:
满足条件: ,
, .
.
(I)若 ,
,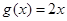 ,
, ,
, 存在,求
存在,求 的取值范围;
的取值范围;
(II)若函数 为
为 上的增函数,
上的增函数, ,
, ,
, ,证明对任意
,证明对任意 ,
, (用
(用 表示).
表示).
查看答案和解析>>
科目: 来源:2007年普通高等学校招生全国统一考试理科数学卷(江西) 题型:解答题
(本小题满分14分)
设正整数数列{an}满足:a2=4,且对于任何
n∈N*,有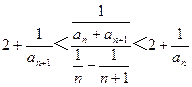 .
.
(1)求a1,a3;
(2)求数列{ an }的通项an.
查看答案和解析>>
科目: 来源:2007年普通高等学校招生全国统一考试理科数学卷(山西) 题型:解答题
(本小题满分12分)
已知数列{an}中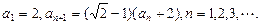
(Ⅰ)求{an}的通项公式;
(Ⅱ)若数列{bn}中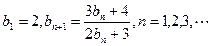 ,证明:
,证明: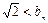 ≤
≤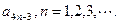
查看答案和解析>>
科目: 来源:2007年普通高等学校招生全国统一考试文科数学卷(湖南) 题型:解答题
(本小题满分13分)
设 是数列
是数列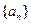 (
(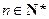 )的前
)的前 项和,
项和, ,且
,且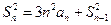 ,
, ,
, .
.
(I)证明:数列 (
(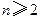 )是常数数列;
)是常数数列;
(II)试找出一个奇数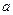 ,使以18为首项,7为公比的等比数列
,使以18为首项,7为公比的等比数列 (
(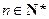 )中的所有项都是数列
)中的所有项都是数列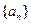 中的项,并指出
中的项,并指出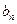 是数列
是数列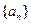 中的第几项.
中的第几项.
查看答案和解析>>
科目: 来源:2007年普通高等学校招生全国统一考试文科数学卷(天津) 题型:解答题
(本小题满分14分)
在数列 中,
中, ,其中
,其中 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和 ;
;
(Ⅲ)证明存在 ,使得
,使得 对任意
对任意 均成立.
均成立.
查看答案和解析>>
科目: 来源:2007年普通高等学校招生全国统一考试理科数学卷广东 题型:解答题
(本题满分14分)
已知函数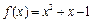 ,
,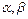 是方程f(x)=0的两个根
是方程f(x)=0的两个根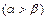 ,
,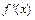 是f(x)的导数.
是f(x)的导数.
设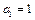 ,
,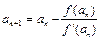 (n=1,2,……)
(n=1,2,……)
(1)求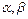 的值;
的值;
(2)证明:对任意的正整数n,都有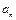 >a;
>a;
(3)记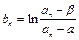 (n=1,2,……),求数列{bn}的前n项和Sn。
(n=1,2,……),求数列{bn}的前n项和Sn。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com