
科目: 来源:2011届甘肃省天水市一中高三上学期第一阶段性考试理科数学卷 题型:解答题
(本小题满分12分)
数列 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意
项和,对于任意 ,总有
,总有 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 设正数数列 满足
满足 ,求数列
,求数列 中的最大项;
中的最大项;
查看答案和解析>>
科目: 来源:2011届江苏省苏州市红心中学高三摸底考试数学卷 题型:解答题
(本小题满分12分)在直角坐标平面上有一点列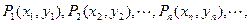 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数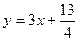 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以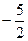 为首项,-1为公差的等
为首项,-1为公差的等 差数列{xn}.
差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,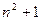 ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求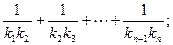
(3) 设
设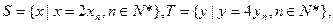 等差数列
等差数列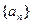 的任一项
的任一项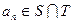 ,其中
,其中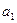 是
是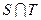 中的最大数,
中的最大数,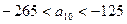 ,求数列
,求数列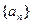 的通项公式.
的通项公式.
查看答案和解析>>
科目: 来源:2011届安徽师大附中高三第一次模拟考试文科数学卷 题型:解答题
(本小题满分12分)
已知数列 中,
中, 是其前
是其前 项和,并且
项和,并且 ,
,
⑴设数列 ,求证:数列
,求证:数列 是等比数列;
是等比数列;
⑵设数列 ,求证:数列
,求证:数列 是等差数列;
是等差数列;
⑶求数列 的通项公式及前
的通项公式及前 项和。
项和。
查看答案和解析>>
科目: 来源:广州省高州一中2009-2010学年高二学科竞赛(数学文) 题型:解答题
(本小题满分14分)已知函数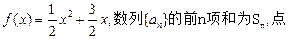
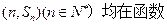
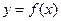 的图象上。
的图象上。
(1)求数列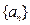 的通项公式
的通项公式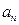 ;
;
(2)令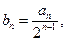 求数列
求数列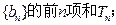
(3)令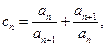 证明:
证明: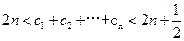 。
。
查看答案和解析>>
科目: 来源:广州省高州一中2009-2010学年高二学科竞赛(数学理) 题型:解答题
(本小题满分14分)
下表给出的是由n×n(n≥3,n∈N*)个正数排成的n行n列数表, 表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为
表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为 ,若已知
,若已知
 |  |  | … |  |
 |  |  | … |  |
 |  |  | … |  |
| … | … | … | … | … |
 |  |  | … |  |
 的值;
的值; 表示
表示 的代数式;
的代数式; ,
, ,
, ,……,
,……, 组成一列数列,设Tn=
组成一列数列,设Tn= +
+ +
+ +……+
+……+ 求使不等式
求使不等式 成立的最小正整数n.
成立的最小正整数n. 查看答案和解析>>
科目: 来源:2011届安徽省皖南八校高三第一次联考理科数学卷 题型:解答题
(本小题满分13分)
在数列 。
。
(1)求证:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式
的通项公式 ;
;
(2)设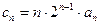 ,求数列
,求数列 的前
的前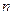 项和。
项和。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com