
科目: 来源:2011届河北省冀州中学高三下学期开学考试数学文卷 题型:解答题
(本小题满分12分)
已知数列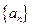 是首项为
是首项为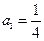 ,公比
,公比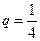 的等比数列,设
的等比数列,设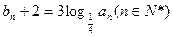 ,数列
,数列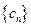 满足
满足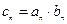 .
.
(Ⅰ)求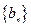 的通项公式;
的通项公式;
(Ⅱ)若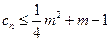 对一切正整数
对一切正整数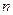 恒成立,求实数
恒成立,求实数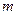 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2011届河北省冀州中学高三上学期期末考试数学文卷 题型:解答题
(
(本小题满分12分)
已知数列 中,
中, ,且当
,且当 时,函数
时,函数 取得极值。
取得极值。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)数列 满足:
满足: ,
, ,证明:
,证明: 是等差数列,并求数列
是等差数列,并求数列 的通项公式通
的通项公式通 项及前
项及前 项和
项和 .
.
查看答案和解析>>
科目: 来源:2011届湖北省荆州中学高三上学期期末考试数学文卷 题型:解答题
(本小题满分14分)
已知数列 满足
满足 ;
;
(1)证明:数列 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式;
的通项公式;
(2)若 求数列
求数列 的前
的前 项和为
项和为 ;
;
(3)令 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
查看答案和解析>>
科目: 来源:2011届四川省资阳市高三第一次高考模拟数学理卷 题型:解答题
(本小题满分12分)
数列 的前n项和为
的前n项和为 ,且
,且 (
( ).
).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列 满足:
满足: (
( ),求数列
),求数列 的通项公式;
的通项公式;
(Ⅲ)设 (
( ),是否存在实数
),是否存在实数 ,使
,使 得当
得当 时,
时, 恒成立?若存在,求出实数
恒成立?若存在,求出实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2011届上海市浦东新区高三第一学期质量抽测数学理卷 题型:解答题
(本小题满分16分,第1小题满分4分,第2小题满分5分,第3小
题满分7分)
(1)若对于任意的 ,总有
,总有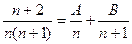 成立,求常数
成立,求常数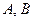 的值;
的值;
(2)在数列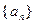 中,
中,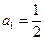 ,
, (
(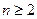 ,
,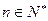 ),求通项
),求通项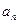 ;
;
(3)在(2)题的条件下,设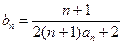 ,从数列
,从数列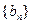 中依次取出第
中依次取出第 项,第
项,第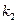 项,…第
项,…第 项,按原来的顺序组成新
项,按原来的顺序组成新 的数列
的数列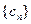 ,其中
,其中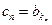 ,其中
,其中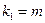 ,
,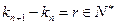 .试问是否存在正整数
.试问是否存在正整数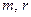 使
使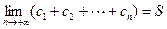 且
且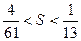 成立?若存
成立?若存 在,求正整数
在,求正整数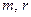 的值;不存在,说明理由.
的值;不存在,说明理由.
查看答案和解析>>
科目: 来源:2011届北京市朝阳区高三上学期期末理科数学卷 题型:解答题
已知函数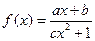 (
(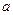 ,
,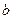 ,
,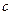 为常数,
为常数,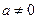 ).
).
(Ⅰ)若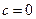 时,数列
时,数列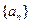 满足条件:点
满足条件:点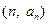 在函数
在函数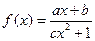 的图象上,求
的图象上,求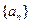 的前
的前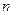 项和
项和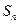 ;
;
(Ⅱ)在(Ⅰ)的条件下,若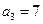 ,
,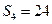 ,
,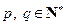 (
(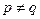 ),
),
证明: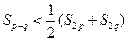 ;
;
(Ⅲ)若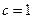 时,
时,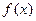 是奇函数,
是奇函数,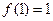 ,数列
,数列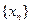 满足
满足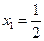 ,
,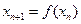 ,
,
求证: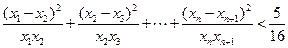 .
.
查看答案和解析>>
科目: 来源:2011届上海市徐汇区高三上学期期末理科数学卷 题型:解答题
各项均为正数的数列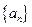 的前
的前 项和为
项和为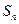 ,满足
,满足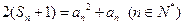
(1)求数列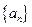 的通项公式;
的通项公式;
(2)若数列 满足
满足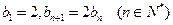 ,
,
数列 满足
满足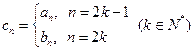 ,数列
,数列 的前
的前
 项和为
项和为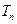 ,求
,求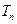 ;
;
(3)若数列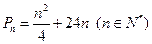 ,甲同学利用第(2)问中的
,甲同学利用第(2)问中的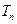 ,试图确定
,试图确定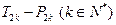 的值是否可以等于2011?为此,他设计了一个程序
的值是否可以等于2011?为此,他设计了一个程序 (如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。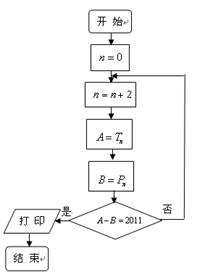
查看答案和解析>>
科目: 来源:2011届江苏省常州市教育学会高三学生学业水平监测数学试卷 题型:解答题
(本小题满分16分)
已知数列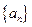 满足
满足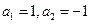 ,当
,当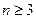 ,
,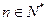 时,
时, .
.
⑴求数列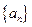 的通项公式;
的通项公式;
⑵是否存在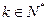 ,使得
,使得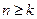 时,不等式
时,不等式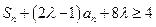 对任意实数
对任意实数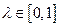 恒成立?若存在,求出
恒成立?若存在,求出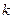 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
⑶在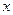 轴上是否存在定点
轴上是否存在定点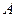 ,使得三点
,使得三点 、
、 、
、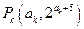 (其中
(其中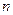 、
、 、
、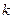 是互不相等的正整数且
是互不相等的正整数且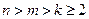 )到定点
)到定点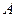 的距离相等?若存在,求出点
的距离相等?若存在,求出点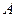 及正整数
及正整数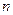 、
、 、
、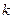 ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2011届辽宁省铁岭六校高三上学期第三次联考数学文卷 题型:解答题
设数列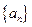 前
前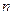 项和为
项和为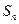 ,点
,点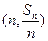
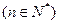 均在函数
均在函数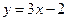 图象上。
图象上。
(1)求数列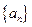 的通
的通 项公式;
项公式;
(2)设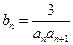 ,
,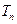 是数列
是数列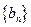 的前
的前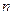 项和,求使得
项和,求使得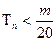 对所有
对所有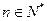 都成立的最小正整数
都成立的最小正整数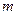 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com