
科目: 来源:2012届新人教版高三上学期单元测试(5)数学试卷 题型:解答题
(14分)给出 下面的数表序列:
下面的数表序列:
其中表n(n="1,2,3"  )有n行,第1行的n个数是1,3,5,
)有n行,第1行的n个数是1,3,5, 2n-1,从第2行起
2n-1,从第2行起 ,每行中的每个数都等
,每行中的每个数都等 于它肩上的两数之和。
于它肩上的两数之和。
(I)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明);
(II)每个数列中最后一行都只有一个数,它们构成数列1,4,12
 ,记此数列为
,记此数列为 求和:
求和:

查看答案和解析>>
科目: 来源:2012届新人教版高三上学期单元测试(5)数学试卷 题型:解答题
(14分)设各项均为正数的数列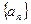 的前n项和为
的前n项和为 ,已知
,已知 ,数
,数
列 是公差为
是公差为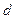 的等差数列。
的等差数列。
(1)求数列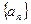 的通项公式(用
的通项公式(用 表示);
表示);
(2)设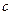 为实数,对满足
为实数,对满足 的任意正整数
的任意正整数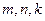 ,不等式
,不等式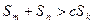 都成立。求证:
都成立。求证: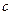 的最大值为
的最大值为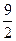 。
。
查看答案和解析>>
科目: 来源:2012届新人教版高三上学期单元测试(5)数学试卷 题型:解答题
(12分)设

 ,若将
,若将
适当排序后可构成公差为1的等差数列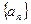 的前三项.
的前三项.
(Ⅰ)求
 的值及
的值及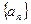 的通项公式;
的通项公式;
(Ⅱ )记函数
)记函数 的图象在
的图象在 轴上截得的线段长为
轴上截得的线段长为 ,设
,设 ,求
,求
查看答案和解析>>
科目: 来源:2012届浙江省温州市十校联合体高三上学期期初摸底文科数学 题型:解答题
(本题满分14分)等 比数列
比数列 中,已知
中,已知
1)求数列 的通项
的通项
2)若等差数列 ,
, ,求数列
,求数列 前n项和
前n项和 ,并求
,并求 最大值
最大值
查看答案和解析>>
科目: 来源:2011-2012学年黑龙江省大庆实验中学高二上学期开学考试文科数学 题型:解答题
(本小题满分12分)设数列 满足:
满足: ,
,
(Ⅰ)求证: ;
;
(Ⅱ)若 ,对任意的正整数
,对任意的正整数 ,
, 恒成
恒成
立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2012届山东省曲阜师大附中高三9月月考理科数学 题型:解答题
.(本小题满分12分)已知数列 的各项均是正数,其前
的各项均是正数,其前 项和为
项和为 ,满足
,满足 ,其中
,其中 为正常数,且
为正常数,且
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:
查看答案和解析>>
科目: 来源:2012届山东省兖州市高三入学摸底考试理科数学 题型:解答题
(本小题满分12分)
已知等差数列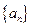 满足:
满足: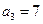 ,
,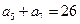 ,
,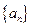 的前n项和为
的前n项和为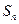 .
.
(Ⅰ)求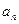 及
及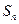 ;
;
(Ⅱ)令bn=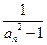 (
(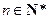 ),求数列
),求数列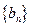 的前n项和
的前n项和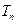 .
.
查看答案和解析>>
科目: 来源:2012届四川省成都外国语学校高三8月月考数学 题型:解答题
(本小题满分12分)
设数列{an}的首项a1∈(0,1),an+1=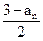 (n∈N+)
(n∈N+)
(I)求{an}的通项公式
(II)设bn=an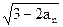 ,判断数列{bn}的单调性,并证明你的结论
,判断数列{bn}的单调性,并证明你的结论
查看答案和解析>>
科目: 来源:2010-2011学年新疆乌鲁木齐八中高一下学期期末考试数学 题型:解答题
已知数列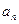 的各项均为正数,
的各项均为正数,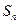 为其前n项和,对于任意的
为其前n项和,对于任意的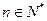 ,满足关系式
,满足关系式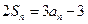
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的通项公式是
的通项公式是 ,求
,求 的前n项和为
的前n项和为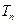 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com