
科目: 来源:2010年广东省广州市番禺区高二下学期期中考试数学(理) 题型:解答题
(14分)四棱锥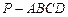 的底面
的底面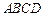 是正方形,侧棱
是正方形,侧棱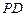 ⊥底面
⊥底面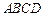 ,
,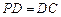 ,
,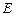 是
是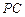 的中点.
的中点.
(1)证明 //平面
//平面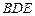 ;
;
(2)求二面角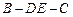 的平面角的余弦值;
的平面角的余弦值;
(3)在棱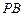 上是否存在点
上是否存在点 ,使
,使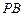 ⊥平面
⊥平面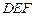 ?
?
若存在,请求出 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.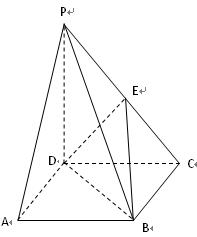
查看答案和解析>>
科目: 来源:2010届广东华南师范大学附属中学高三模拟数学试题(三) 题型:解答题
(满分12分)正方体ABCD-A1B1C1D1 的棱长为 2,且AC 与BD 交于点O,E 为棱DD1 中点,以A 为原点,建立空间直角坐标系A-xyz,如图所示.
(Ⅰ)求证:B1O⊥平面EAC;
(Ⅱ)若点  F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
(Ⅲ)求二面角B1-EA-C 的正弦值.
查看答案和解析>>
科目: 来源:2010年广东省广州市番禺区高二下学期期中考试数学(文) 题型:解答题
(13分)如图,在直三棱柱 中,
中, ,
, 。
。
(1)求证: ;(2)已知
;(2)已知 是棱
是棱 上的一动点,问:三棱锥
上的一动点,问:三棱锥 的体积是否为定值,如不是定值,请说明理由;如是定值,请求出此定值。
的体积是否为定值,如不是定值,请说明理由;如是定值,请求出此定值。
查看答案和解析>>
科目: 来源:2010年浙东北三校高二下学期期中联考数学(理) 题型:解答题
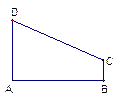
如图,直角梯形 中,
中,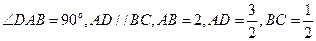
椭圆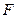 以
以 为焦点且过点
为焦点且过点 ,
,
(1)建立适当的直角坐标系,求椭圆的方程;
(2)若点E满足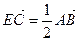 是否存在斜率
是否存在斜率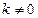 的直线
的直线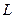 与椭圆
与椭圆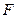 交于
交于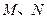 两点,且
两点,且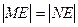 ,若存在,求
,若存在,求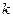 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
查看答案和解析>>
科目: 来源:2010年辽宁省大连市高三第二次模拟考试数学(文) 题型:解答题
(本小题满分12分)如图4,四棱锥P—ABCD中,底面ABCD是直角梯形,AB//CD,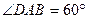 ,AB=AD=2CD,侧面
,AB=AD=2CD,侧面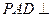 底面ABCD,且
底面ABCD,且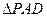 为等腰直角三角形,
为等腰直角三角形,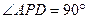 ,M为AP的中点。
,M为AP的中点。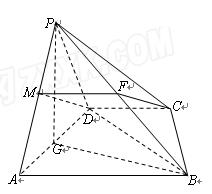
(1)求证: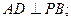
(2)求证:DM//平面PCB。
查看答案和解析>>
科目: 来源:四川省成都七中高三数学一诊模拟测试理科 题型:解答题
(12分)如图,在四棱椎 中,底面
中,底面 是
是 且边长为2的菱形,
且边长为2的菱形, 侧面
侧面 为正三角形,其所在平面垂直于底面
为正三角形,其所在平面垂直于底面 .
.
(1)若G为 边的中点,求证:
边的中点,求证: 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
(3)若E为 的中点,能否在棱
的中点,能否在棱 上找一点F,使得平面
上找一点F,使得平面 平面
平面 ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目: 来源:2010年吉林省东北师大附中高一下学期期中考试数学 题型:解答题
(本题满分10分)
如图,在四边形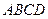 中,
中,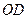 垂直平分
垂直平分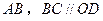 ,且
,且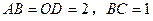 ,现将四边形
,现将四边形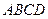 沿
沿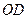 折成直二面角,求:
折成直二面角,求:
(1)求二面角 的正弦值;
的正弦值;
(2)求三棱锥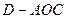 的体积.
的体积.
查看答案和解析>>
科目: 来源:2010年河北省正定中学高二下学期期中考试数学(文) 题型:解答题
(本小题满分12分)
已知三棱柱 中,各棱长均为2,平面
中,各棱长均为2,平面 ⊥平 面
⊥平 面 ,
, .
.
(1)求证: ⊥平面
⊥平面 ;
;
(2)求二面角 的大小;
的大小;
查看答案和解析>>
科目: 来源:2010年江苏省启东中学高二下学期期中考试数学(理) 题型:解答题
(16分)如图,w*w^w.k&s#5@u.c~o*m四棱锥S-ABCD的底面是正方形,每条侧棱的长都是地面边长的 倍,
倍,
P为侧棱SD上的点。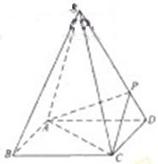
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E,使得BE∥平
面PAC。若存在,求SE:EC的值 ;若不存在,试说明理由。
;若不存在,试说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com