
科目: 来源:2011年浙东北三校高二上学期期中考试数学试卷 题型:解答题
. (本小题满分9分)
(如图)在底面为平行四边形的四棱锥 中,
中, ,
, 平面
平面 ,且
,且 ,点
,点 是
是 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)(理科学生做)求二面角 的大小.
的大小.
(文科学生做)当 ,
, 时,求直线
时,求直线 和平面
和平面 所成的线面角的大小.
所成的线面角的大小.
查看答案和解析>>
科目: 来源:2011届四川省成都外国语学校高三下学期3月月考数学理卷 题型:解答题
((本小题满分12分)
如图所示,多面体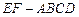 中,
中, 是梯形,
是梯形,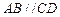 ,
,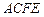 是矩形,平面
是矩形,平面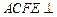 平面
平面 ,
, ,
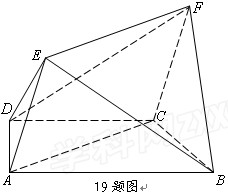
,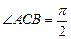 。
。
(1)求证: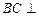 平面
平面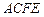 ;
;
(2)若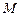 是棱
是棱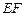 上一点,
上一点,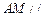 平面
平面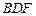 ,求
,求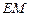 ;
;
(3)求二面角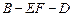 的平面角的余弦值。
的平面角的余弦值。
查看答案和解析>>
科目: 来源:2011山西省忻州市高二上学期联考数学理卷A 题型:解答题
(.(本小题满分12分)
如图,四棱锥S-ABCD的底面是矩形,AB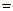 a,AD
a,AD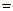 2,SA
2,SA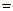 1,且SA⊥底面ABCD,若
1,且SA⊥底面ABCD,若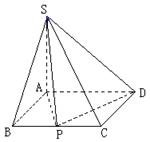
边BC上存在异于B,C的一点P,使得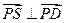 .
.
(1)求a的最大值;
(2)当a取最大值时,求平面SCD的一 个单位法向量
个单位法向量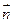
及点P到平面SCD的距离.
查看答案和解析>>
科目: 来源:2011届甘肃省天水一中高三一模调研考试数学理卷 题型:解答题
(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是正方形,PA⊥平面ABCD,且PA=AB=2,E、F分别为AB、PC的中点。
(1)求异面直线PA与BF所成角的正切值。
(2) 求证:EF⊥平面PCD。
求证:EF⊥平面PCD。
查看答案和解析>>
科目: 来源:2011届江苏省苏、锡、常、镇四市高三调研测试数学卷(一) 题型:解答题
如图, 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰 的长为
的长为 (百米),底
(百米),底 的长为
的长为 (百米).现决定在空地内筑一条笔直的小路
(百米).现决定在空地内筑一条笔直的小路 (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为 和
和 .
.
⑴若小路一端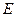 为
为 的中点,求此时小路的长度;
的中点,求此时小路的长度;
⑵求 的最小值.
的最小值.
查看答案和解析>>
科目: 来源:2011届浙江省六校高三2月月考数学理卷 题型:解答题
(本题满分14分)
如图,正方形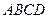 所在平面与圆
所在平面与圆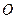 所在平面相交于
所在平面相交于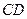 ,线段
,线段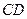 为圆
为圆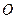 的弦,
的弦,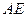 垂直于圆
垂直于圆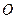 所在平面,垂足
所在平面,垂足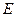 是圆
是圆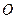 上异于
上异于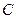 、
、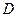 的点,
的点,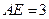 ,圆
,圆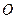 的直径为9
的直径为9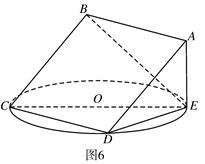
(Ⅰ)求证:平面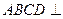 平面
平面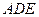 ;
;
(Ⅱ)求二面角 的平面角的正切值。
的平面角的正切值。
查看答案和解析>>
科目: 来源:2011届广东省揭阳市第一中学高三调研检测数学理卷 题型:解答题
(本题满分14分)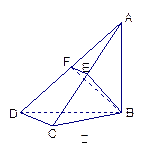
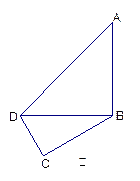
如图甲,在平面四边形ABCD中,已知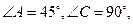
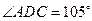 ,
,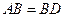 ,现将四边形ABCD沿BD折起,
,现将四边形ABCD沿BD折起,
使平面ABD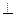 平面BDC(如图乙),设点E、F分别为棱
平面BDC(如图乙),设点E、F分别为棱
AC、AD的中点.
(1)求证:DC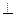 平面ABC;
平面ABC;
(2)求BF与平面ABC所成角的正弦;
(3)求二面角B-EF-A的余弦.
查看答案和解析>>
科目: 来源:2011届广东省华南师大附中高三综合测试数学理卷 题型:解答题
(本题满分14分) 已知矩形ABCD,AD=2AB=2,点E是AD的中点,将△DEC
沿CE折起到△D’EC的位置,使二面角D'-EC -B是直二面角。
(Ⅰ) 证明:BE⊥CD’;
(Ⅱ) 求二面角D'-BC -E的余弦值,
查看答案和解析>>
科目: 来源:2011年河北省正定中学高二上学期期末考试数学试卷 题型:解答题
(本小题满分12分)
已知梯形ABCD中,AD∥BC,∠ABC ="∠BAD" = ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
(I)当x=2时,求证:BD⊥EG ;
(II)若以F、B、C、D为顶点的三棱锥的体积记为 ,
,
求 的最大值;
的最大值;
(III)当 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.
[来源:学科网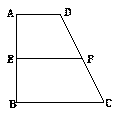 ZXXK
ZXXK ]
]
查看答案和解析>>
科目: 来源:2011届河北省冀州中学高三第一次模拟考试数学理卷 题型:解答题
(本小题满分12分)
已知平行六面体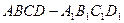 的底面为正方形,
的底面为正方形,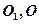 分别为上、下底面的中心,且
分别为上、下底面的中心,且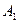 在底面
在底面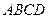 的射影是
的射影是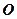 。
。 (Ⅰ)求证:平面
(Ⅰ)求证:平面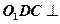 平面
平面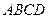 ;
;
(Ⅱ)若点 分别在棱上
分别在棱上 上,且
上,且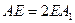 ,问点
,问点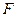 在何处时,
在何处时,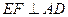 ;
;
(Ⅲ)若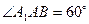 ,求二面角
,求二面角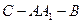 的大小(用反三角函数表示)。
的大小(用反三角函数表示)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com