
科目: 来源:宁波市2010届高三三模考试文科数学试题 题型:解答题
(本小题15分)已知抛物线 ,过点
,过点 的直线
的直线 交抛物线
交抛物线 于
于 两点,且
两点,且 .
.
(1)求抛物线 的方程;
的方程;
(2)过点 作
作 轴的平行线与直线
轴的平行线与直线 相交于点
相交于点 ,若
,若 是等腰三角形,求直线
是等腰三角形,求直线 的方程.
的方程.
查看答案和解析>>
科目: 来源:杭州市2010年第二次高考科目教学质量检测 题型:解答题
(本题满分15分)已知直线 ,曲线
,曲线
(1)若 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数 的取值;
的取值;
(2)若 ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]
查看答案和解析>>
科目: 来源:2008年普通高等学校招生全国统一考试数学文史类(福建卷) 题型:解答题
(本小题满分14分)
如图,椭圆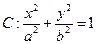 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.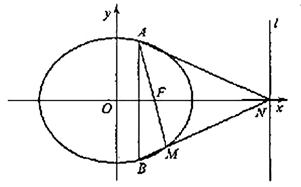
查看答案和解析>>
科目: 来源:北京市宣武区2010年高三第一次质量检测数学(文)试题 题型:解答题
(本小题共14分)
已知椭圆的中点在原点O,焦点在x轴上,点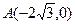 是其左顶点,点C在椭圆上且
是其左顶点,点C在椭圆上且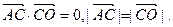
(I)求椭圆的方程;
(II)若平行于CO的直线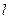 和椭圆交于M,N两个不同点,求
和椭圆交于M,N两个不同点,求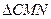 面积的最大值,并求此时直线
面积的最大值,并求此时直线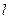 的方程.
的方程.
查看答案和解析>>
科目: 来源:长葛市第三实验高中2010年高考模拟试卷(1) 题型:解答题
(本小题共12分)
在直角坐标系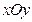 中,动点P到两定点
中,动点P到两定点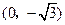 ,
,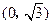 的距离之和等于4,设动点P的轨迹为
的距离之和等于4,设动点P的轨迹为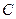 ,过点
,过点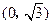 的直线与
的直线与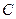 交于A,B两点.
交于A,B两点.
(1)写出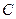 的方程;
的方程;
(2)设d为A、B两点间的距离,d是否存在最大值、最小值;若存在,求出d的最大值、最小值.
查看答案和解析>>
科目: 来源:广东省揭阳市2010年高考一模(文) 题型:解答题
(本题满分14分)
在平面直角坐标系中,已知向量 (
( ),
), ,动点
,动点 的轨迹为T.
的轨迹为T.
(1)求轨迹T的方程,并说明该方程表示的曲线的形状;
(2)当 时,已知
时,已知 、
、 ,试探究是否存在这样的点
,试探究是否存在这样的点 :
: 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目: 来源:唐河三高2010届高三第一次模拟数学文科 题型:解答题
(本小题共13分)
在平面直角坐标系xOy中,经过点(0, 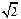 )且斜率为k的直线l与椭圆
)且斜率为k的直线l与椭圆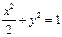 有两个不同的交点P和Q.
有两个不同的交点P和Q.
(Ⅰ)求k的取值范围;
(Ⅱ)设椭圆与x轴正半轴、y轴正半轴的交点分别为A,B,是否存在常数k,使得向量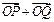 与
与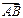 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源:2008年普通高等学校招生全国统一考试文科数学(重庆卷) 题型:解答题
(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分.)
如题(21)图,M(-2,0)和N(2,0)是平面上的两点,动点P满足: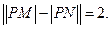
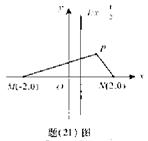
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设d为点P到直线l: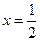 的距离,若
的距离,若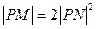 ,求
,求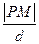 的值.
的值.
查看答案和解析>>
科目: 来源:浏阳一中、田中高三年级2009年下期期末联考试题 数学试题 题型:解答题
(本小题12分)
如图,曲线 是以原点
是以原点 为中心,以
为中心,以 、
、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以 为顶点,以
为顶点,以 为焦点的抛物线的一部分,
为焦点的抛物线的一部分, 是曲线
是曲线 和
和 的交点,且
的交点,且 为钝角,若
为钝角,若 ,
, .
.
(I)求曲线 和
和 所在的椭圆和抛物线的方程;
所在的椭圆和抛物线的方程;
(II)过 作一条与轴不垂直的直线,分别与曲线
作一条与轴不垂直的直线,分别与曲线 、
、 依次交于
依次交于 、
、 、
、 、
、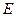 四点(如图),若
四点(如图),若 为
为 的中点,
的中点, 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源:2011-2012年福建省四地六校高二第二次月考理科数学 题型:填空题
如图,P是双曲线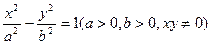 上的动点,
上的动点,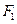 、
、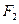 是双曲线的左右焦点,
是双曲线的左右焦点,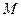 是
是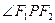 的平分线上一点
的平分线上一点 ,且
,且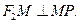 某同学用以下方法研究
某同学用以下方法研究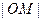 :延长
:延长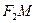 交
交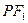 于点
于点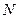 ,可知
,可知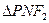 为等腰三角形,且M为
为等腰三角形,且M为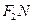 的中点,得
的中点,得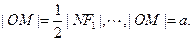 类似地:P是椭圆
类似地:P是椭圆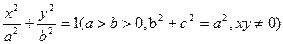 上的动点,
上的动点,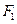 、
、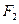 是椭圆的左右焦点,M是
是椭圆的左右焦点,M是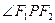 的平分线上一点,且
的平分线上一点,且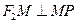 ,则
,则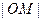 的取值范围是 .
的取值范围是 .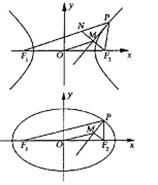
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com