
科目: 来源:2011年普通高中招生考试北京市高考文科数学 题型:解答题
(本小题共14分)
已知椭圆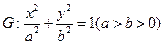 的离心率为
的离心率为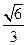 ,右焦点为
,右焦点为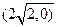 。斜率为1的直线
。斜率为1的直线 与椭圆
与椭圆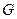 交于
交于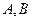 两点,以
两点,以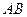 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为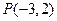 。
。
(Ⅰ)求椭圆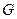 的方程;
的方程;
(Ⅱ)求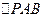 的面积。
的面积。
查看答案和解析>>
科目: 来源:2010~2011学年浙江省杭州二中高三6月考前冲刺卷数学理 题型:解答题
(本小题满分15分)
已知椭圆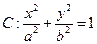
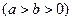 的离心率为
的离心率为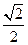 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线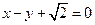 相切.
相切.
(Ⅰ)求椭圆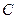 的方程;
的方程;
(Ⅱ)若过点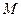 (2,0)的直线与椭圆
(2,0)的直线与椭圆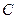 相交于两点
相交于两点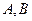 ,
,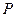 为椭圆上一点,且满足
为椭圆上一点,且满足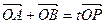 (
(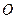 为坐标原点),当
为坐标原点),当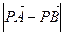 <
<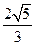 时,求实数
时,求实数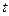 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2010-2011学年安徽省亳州市涡阳二中高二第二学期期末质量检测文科数学试题 题型:解答题
已知双曲线 与椭圆
与椭圆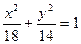 有共同的焦点,点
有共同的焦点,点 在双曲线C上.
在双曲线C上.
(1)求双曲线C的方程;
(2)以P(1,2)为中点作双曲线C的一条弦AB,求弦AB所在直线的方程.
查看答案和解析>>
科目: 来源:2011年辽宁省普通高等学校招生统一考试理科数学 题型:解答题
本小题满分12分)
如图,已知椭圆C1的中心在原点O,长轴左、右端点M,N在x轴上,椭圆C2的短轴为MN,且C1,C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点按纵坐标从大到小依次为A,B,C,D.
(I)设 ,求
,求 与
与 的比值;
的比值;
(II)当e变化时,是否存在直线l,使得BO∥AN,并说明理由
查看答案和解析>>
科目: 来源:2011年陕西省普通高等学校招生统一考试理科数学 题型:解答题
(本小题满分12分)如图,从点 作
作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 ,曲线在
,曲线在 点处的切线与
点处的切线与 轴交于点
轴交于点 ,再从
,再从 作
作 轴的垂线交曲线于点
轴的垂线交曲线于点 ,依次重复上述过程得到一系列点:
,依次重复上述过程得到一系列点: ,
, ;
; ,
, ;
; ;
; ,
, 记
记 点的坐标为
点的坐标为 (
( )
)
(Ⅰ)试求 与
与 的关系(
的关系( )
)
(Ⅱ)求
查看答案和解析>>
科目: 来源:2010-2011学年河北冀州中学高二年级下学期第三次月考题(文) 题型:解答题
已知椭圆 (a>b>0)的离心率e=
(a>b>0)的离心率e= ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l与椭圆相交于不同的两点A、B,已知点A的坐标为
(i)若 ,求直线l的倾斜角;
,求直线l的倾斜角;
(ii)若点Q 在线段AB的垂直平分线上,且
在线段AB的垂直平分线上,且 .求
.求 的值.
的值.
查看答案和解析>>
科目: 来源:2010-2011学年河北冀州中学高二年级下学期第三次月考题(理) 题型:解答题
已知椭圆C: 的长轴长为
的长轴长为 ,离心率
,离心率 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若过点B(2,0)的直线 (斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且
(斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且 OBE与
OBE与 OBF的面积之比为
OBF的面积之比为 , 求直线
, 求直线 的方程.
的方程.
查看答案和解析>>
科目: 来源:2011年江西省普通高中招生考试理科数学 题型:解答题
(本小题满分13分) 是双曲线
是双曲线 :
: 上一点,
上一点, 分别是双曲线
分别是双曲线 的左、右定点,直线
的左、右定点,直线 的斜率之积为
的斜率之积为 .
.
(1)求双曲线的离心率;
(2)过双曲线 的右焦点且斜率为1的直线交双曲线于
的右焦点且斜率为1的直线交双曲线于 两点,
两点, 为坐标原点,
为坐标原点, 为双曲线上的一点,满足
为双曲线上的一点,满足 ,求
,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com