
科目: 来源:2010-2011学年河北省冀州中学高二下学期期末考试理科数学(B卷) 题型:解答题
(12分)已知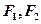 分别是椭圆
分别是椭圆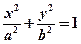
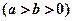 的左、右 焦点,已知点
的左、右 焦点,已知点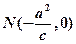 满足
满足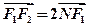 ,且
,且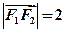 。设
。设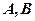 是上半椭圆上且满足
是上半椭圆上且满足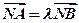 的两点。
的两点。
(1)求此椭圆的方程;
(2)若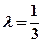 ,求直线AB的斜率。
,求直线AB的斜率。
查看答案和解析>>
科目: 来源:山东省邹城一中10-11学年高二下学期期末考试数学(理) 题型:解答题
已知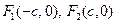 是椭圆
是椭圆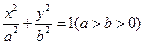 的左、右焦点,过点
的左、右焦点,过点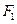 作
作
倾斜角为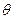 的动直线
的动直线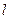 交椭圆于
交椭圆于 两点.当
两点.当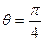 时,
时,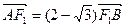 ,且
,且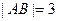 .
.
(1)求椭圆的离心率及椭圆的标准方程;
(2)求△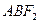 面积的最大值,并求出使面积达到最大值时直线
面积的最大值,并求出使面积达到最大值时直线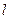 的方程.
的方程.
查看答案和解析>>
科目: 来源:上海交通大学附属中学2010-2011学年度高二下学期期末考试数学 题型:解答题
(本题满分16分)第一题满分4分,第二题满分6分,第三题满分6分.
已知动圆过定点P(1,0),且与定直线 相切。
相切。
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且倾斜角为 的直线与曲线M相交于A,B两点,A,B在直线
的直线与曲线M相交于A,B两点,A,B在直线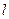 上的射影是
上的射影是 。求梯形
。求梯形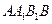 的面积;
的面积;
(3)若点C是(2)中线段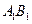 上的动点,当△ABC为直角三角形时,求点C的坐标。
上的动点,当△ABC为直角三角形时,求点C的坐标。
查看答案和解析>>
科目: 来源:海南省海南中学10-11学年高一下学期期末考试数学(1班) 题型:解答题
(本题满分14分)在直角坐标系xOy中,椭圆C1: 的左、右焦点分别为F1、F2.F2也是抛物线C2:
的左、右焦点分别为F1、F2.F2也是抛物线C2: 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且 .
.
(Ⅰ)求C1的方程;
(Ⅱ)平面上的点N满足 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若 ·
· =0,求直线l的方程.
=0,求直线l的方程.
查看答案和解析>>
科目: 来源:海南省海南中学10-11学年高一下学期期末考试数学(1班) 题型:解答题
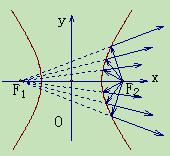
(本题满分12分)阅读下列材料,解决数学问题.圆锥曲线具有非常漂亮的光学性质,被人们广泛地应用于各种设计之中,比如椭圆镜面用来制作电影放映机的聚光灯,抛物面用来制作探照灯等,它们的截面分别是椭圆和抛物线.双曲线也具有非常好的光学性质,从双曲线的一个焦点发出的光线,经过双曲线反射后,反射光线是发散的,它们好像是从另一个焦点射出的一样,如图(1)所示.反比例函数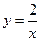 的图像是以直线
的图像是以直线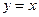 为轴,以坐标轴为渐近线的等轴双曲线,记作C.
为轴,以坐标轴为渐近线的等轴双曲线,记作C.
(Ⅰ)求曲线C的离心率及焦点坐标;
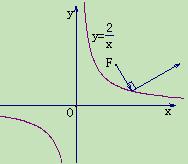
(Ⅱ)如图(2),从曲线C的焦点F处发出的光线经双曲线反射后得到的反射光线与入射光线垂直,求入射光线的方程.
(1) (2)
(2) 
查看答案和解析>>
科目: 来源:海南省海南中学10-11学年高一下学期期末考试数学(1班) 题型:解答题
(本题满分10分)一座抛物线拱桥在某时刻水面的宽度为52米,拱顶距离水面6.5米.
(Ⅰ)建立如图所示的平面直角坐标系xOy,试求拱桥所在抛物线的方程;
(Ⅱ)若一竹排上有一4米宽6米高的大木箱,问此木排能否安全通过此桥?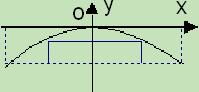
查看答案和解析>>
科目: 来源:吉林省长春十一中10-11学年高二下学期期末考试数学(理) 题型:解答题
已知 是椭圆
是椭圆 的左、右焦点,过点
的左、右焦点,过点 作
作
倾斜角为 的动直线
的动直线 交椭圆于
交椭圆于 两点.当
两点.当 时,
时, ,且
,且 .
.
(1)求椭圆的离心率及椭圆的标准方程;
(2)求△ 面积的最大值,并求出使面积达到最大值时直线
面积的最大值,并求出使面积达到最大值时直线 的方程.
的方程.
查看答案和解析>>
科目: 来源:吉林省长春十一中10-11学年高二下学期期末考试数学(文) 题型:解答题
已知 是椭圆
是椭圆 的左、右焦点,过点
的左、右焦点,过点 作
作
倾斜角为 的直线
的直线 交椭圆于
交椭圆于 两点,
两点, .
.
(1)求椭圆的离心率;
(2)若 ,求椭圆的标准方程.
,求椭圆的标准方程.
查看答案和解析>>
科目: 来源:山东省济南市重点中学10-11学年高二下学期期末考试数学 题型:解答题
(本题满分10分)
已知抛物线 与直线
与直线 相切于点A(1,1)。
相切于点A(1,1)。
(1)求 的解析式;
的解析式;
(2)若对任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源:2010-2011年辽宁省高二下学期期末考试数学理科 题型:解答题
(本小题满分12分)已知点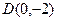 ,过点
,过点 作抛物线
作抛物线
 的切线
的切线 ,切点
,切点 在第二象限,如图.
在第二象限,如图.
(Ⅰ)求切点 的纵坐标;
的纵坐标;
(Ⅱ)若离心率为 的椭圆
的椭圆 恰好经过切点
恰好经过切点 ,设切线
,设切线 交椭圆的另一点为
交椭圆的另一点为 ,记切线
,记切线 的斜率分别为
的斜率分别为 ,若
,若 ,求椭圆方程.
,求椭圆方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com