
科目: 来源:2012届浙江省温州市高三八校联考理科数学 题型:解答题
.本小题满分15分)
如图,已知椭圆E: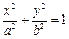
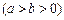 ,焦点为
,焦点为 、
、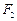 ,双曲线G:
,双曲线G: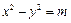
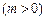 的顶点是该椭
的顶点是该椭 圆的焦点,设
圆的焦点,设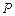 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线 、
、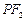 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形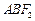 的周长等于
的周长等于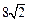 ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为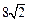 .
.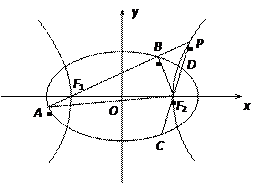
(1)求椭圆E与双曲线G的方程;
(2)设直线 、
、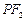 的斜率分别为
的斜率分别为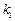 和
和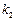 ,探求
,探求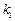 和
和
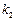 的关系;
的关系;
(3)是否存在常数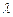 ,使得
,使得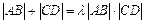 恒成立?
恒成立?
若存在,试求出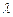 的值;若不存在, 请说明理由.
的值;若不存在, 请说明理由.
查看答案和解析>>
科目: 来源:2012届四川省成都外国语学校高三8月月考数学 题型:解答题
(本小题满分12分)
已知F1(-2,0),F2(2,0),点P满足∣PF1∣-∣PF2∣=2,记点P的轨迹为E.
(I)求轨迹E的方程
(II)若直线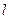 过点F2且与轨迹E交于P,Q两点.无论直线
过点F2且与轨迹E交于P,Q两点.无论直线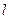 绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
查看答案和解析>>
科目: 来源:2010-2011学年新疆乌鲁木齐八中高二下学期期末考试理科数学 题型:解答题
(10分)已知椭圆 ,其相应于焦点
,其相应于焦点 的准线方
的准线方
程是 ;
;
(1)求椭圆 的方程;
的方程;
(2)已知过点 倾斜角为
倾斜角为 的直线交椭圆
的直线交椭圆 于
于 两点,求弦
两点,求弦 的长度。
的长度。
(3)过点 作两条互相垂直的直线分别交椭圆
作两条互相垂直的直线分别交椭圆 于点
于点 和
和 ,求
,求
的最小值
查看答案和解析>>
科目: 来源:2012届浙江省台州中学高三上学期第一次统练理科数学 题型:解答题
(本题满分10分)已知曲线 上的动点
上的动点 满足到点
满足到点 的距离比到直线
的距离比到直线  的距离小
的距离小 .
.
(1)求曲线 的方程;
的方程;
(2)动点 在直线
在直线  上,过点
上,过点 作曲线
作曲线 的切线
的切线 ,切点分别为
,切点分别为 、
、 .
.
(ⅰ)求证:直线 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;
(ⅱ)在直线 上是否存在一点
上是否存在一点 ,使得
,使得 为等边三角形(
为等边三角形( 点也在直线
点也在直线 上)?若存在,求出点
上)?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2010-2011年陕西省汉中市汉台区高二下学期期末文科数学 题型:解答题
(本小题满分13分)
如图,过抛物线 (
( >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。
⑴设OA的斜率为k,试用k表示点A、B的坐标
⑵求弦AB中点M的轨迹方程
查看答案和解析>>
科目: 来源:2012届云南省昆明一中高三上学期第一次月考试题文科数学 题型:解答题
请考生在第22~24三题中任选一题作答,如果多做,则按所做的第一题记分.
(本小题满分10分)选修4-1:几何证明选讲
如图, 是⊙O的一条切线,切点为
是⊙O的一条切线,切点为 ,
, 都是⊙O的割线,已知
都是⊙O的割线,已知 证明:
证明:
(Ⅰ) ;
;
(Ⅱ)
查看答案和解析>>
科目: 来源:2012届云南省昆明一中高三上学期第一次月考试题文科数学 题型:解答题
(本小题满分12分)
已知双曲线 的离心率为2,焦点到渐近线的距离等于
的离心率为2,焦点到渐近线的距离等于 ,过右焦点
,过右焦点 的直线
的直线
交双曲线于 、
、 两点,
两点, 为左焦点,
为左焦点,
(Ⅰ)求双曲线的方程;
(Ⅱ)若 的面积等于
的面积等于 ,求直线
,求直线 的方程.
的方程.
查看答案和解析>>
科目: 来源:2010-2011年广东省广州市高二下学期期末教学质量检测文科数学 题型:解答题
(本小题满分14分)
在平面直角坐标系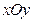 中,已知椭圆
中,已知椭圆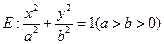 过点
过点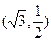 ,且椭圆
,且椭圆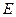 的离心率为
的离心率为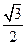
(1)求椭圆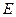 的方程
的方程
(2)是否存在以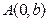 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆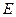 的等腰直角三角形?
的等腰直角三角形? 若存在,求出共有几个;若不存在,请说明理由
若存在,求出共有几个;若不存在,请说明理由
查看答案和解析>>
科目: 来源:2010-2011年广东省广州市高二下学期期末教学质量检测文科数学 题型:解答题
(本小题满分14分)
抛物线 的顶点在原点,焦点F与双曲线
的顶点在原点,焦点F与双曲线 的右焦点重合,过点
的右焦点重合,过点 且斜率为1的直线
且斜率为1的直线 与抛物线
与抛物线 交于
交于 两点
两点
(1)求抛物线 的方程
的方程
(2)求弦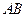 中点到抛物线准线的距离
中点到抛物线准线的距离
查看答案和解析>>
科目: 来源:2010-2011年广东省广州市高二下学期期末教学质量检测理科数学 题型:解答题
(本小题满分14分)
在平面直角坐标系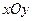 中,已知椭圆
中,已知椭圆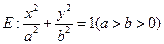 过点
过点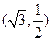 ,且椭圆
,且椭圆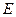 的离心率为
的离心率为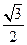 .
.
(1)求椭圆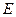 的方程;
的方程;
(2)是否存在以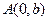 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆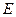 的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com