（本小题满分12分）
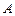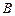将一个半径适当的小球放入如图所示的容器最上方的入口处，小球将自由下落．小球在下落过程中它将3次遇到黑色障碍物，最后落入袋或袋中．已知小球每次遇到黑色障碍物时，向左、右两边下落的概率都是．
（Ⅰ）求小球落入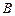袋中的概率；
（Ⅱ）在容器入口处依次放入4个小球，求恰好有3个球落入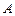袋中的概率．

（本小题满分12分）
将一个半径适当的小球放入如图所示的容器最上方的入口处，小球将自由下落．小球在整个下落过程中它将3次遇到黑色障碍物，最后落入袋或袋中．已知小球每次遇到黑色障碍物时，向左、右两边下落的概率都是．
（Ⅰ）求小球落入袋中的概率；
（Ⅱ）在容器入口处依次放入2个小球，记落入袋中的小球个数为，试求的分布列和的数学期望．

（本小题12分）某公司在过去几年内使用某种型号的灯管1000支，该公司对这些灯管的使用寿命（单位：小时）进行了统计，统计结果如下表所示：

分组	[500，900)	[900，1100)	[1100，1300)	[1300，1500)	[1500，1700)	[1700，1900)	[1900，)
频数	48	121	208	223	193	165	42
频率

（本小题满分12分）
计算机考试分理论考试与上机操作考试两部分进行，每部分考试成绩只记“合格”与“不合格”，两部分考试都“合格”则计算机考试“合格”并颁发“合格证书”.甲、乙、丙三人在理论考试中合格的概率分别为，，；在上机操作考试中合格的概率分别为，，.所有考试是否合格相互之间没有影响.
（Ⅰ）甲、乙、丙三人在同一次计算机考试中谁获得“合格证书”可能性最大？
（Ⅱ）求这三人计算机考试都获得“合格证书”的概率；
(Ⅲ)用表示甲、乙、丙三人在理论考核中合格人数，求的分布列和数学期望.

（本小题满分13分）某人随机地将编号为1,2,3,4的四个小球放入编号为1,2,3,4的四个盒子中，每个盒子放一个小球，全部放完.
（I）求编号为奇数的小球放入到编号为奇数的盒子中的概率；
（II）当一个小球放到其中一个盒子时，若球的编号与盒子的编号相同时，称该球是“放对”的，否则称该球是“放错”的，求至多有2个球“放对”的概率.

一个袋中有若干个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球，得到黑球的概率是；从袋中任意摸出2个球，至少得到1个白球的概率是。
（Ⅰ）若袋中共有10个球，
（i）求白球的个数；Ks5u
（ii）从袋中任意摸出3个球,记得到白球的个数为,求随机变量的数学期望。
（Ⅱ）求证：从袋中任意摸出2个球，至少得到1个黑球的概率不大于。并指出袋中哪种颜色的球个数最少。

（（14分）某突发事件，在不采取任何预防措施的情况下发生的概率为0.3，一旦发生，将造成400万元的损失。现有甲、乙两种相互独立的预防措施可供采用，单独采用甲、乙两种措施所需的费用分别为45万元和30万元，采用相应预防措施后此突发事件不发生的概率为0.9和0.85.若预防方案允许甲乙两种方案单独采用、联合采用或不采用，请确定预防方案使总费用最少。（总费用=采取预防措施的费用+发生突发事件损失的期望值）

（．（12分）在一次购物抽奖活动中，假设某10张券中有一等奖奖券1张，可获价值50元的奖品；有二等奖奖券3张，每张可获价值10元的奖品；其余6张没奖。某顾客从此10张奖券中任抽2张，求：
（1）该顾客中奖的概率；
（2）该顾客获得的奖品总价值X（元）的概率分布列。

（12分）甲、乙两人各进行3次射击，甲每次击中目标的概率为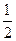，乙每次击中目标的概率为.
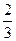（1）记甲击中目标的次数为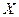，求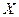的概率分布列及数学期望EX；
（2）求甲恰好比乙多击中目标2次的概率.

(本小题满分10分)已知构成某系统的元件能正常工作的概率为p(0＜p＜1)，且各个元件能否正常工作是相互独立的．今有2n(n大于1)个元件可按如图所示的两种联结方式分别构成两个系统甲、乙．[来源:学科网ZXXK]
(1)试分别求出系统甲、乙能正常工作的概率p₁，p₂；
(2) 比较p₁与p₂的大小，并从概率意义上评价两系统的优劣．