
科目: 来源:2010-2011学年新疆乌鲁木齐八中高二下学期期末考试理科数学 题型:解答题
(10分)体育课进行篮球投篮达标测试。规定:每位同学有5次投篮机会,若
投中3次则“达标”;为节省时间,同时规定:若投篮不到5次已达标,则停止投篮;若即
便后面投篮全中,也不能达标(前3次投中0次)则也停止投篮。同学甲投篮命中率是 ,
,
且每次投篮互不影响。
(1)求同学甲测试达标的概率;
(2)设测试同学甲投篮次数记为 ,求
,求 的分布列及数学期望
的分布列及数学期望 。
。
查看答案和解析>>
科目: 来源:2012届湖南省衡阳市八中高三上学期第一次月考理科数学 题型:解答题
(本小题满分12分) 一个口袋里有5个白球和3个黑球,任意取出一个,如果是黑球,则这个黑球不放回而另外放入一个白球,这样继续下去,直到取出的球是白球时结束取球。求直到取到白球所需的抽取次数 的概率分布列
的概率分布列
查看答案和解析>>
科目: 来源:2012届湖南省衡阳市八中高三上学期第一次月考理科数学 题型:解答题
(本题满分12分)某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如右表所示:
| 付款方式 | 分l期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
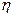 表示经销一辆汽车的利润
表示经销一辆汽车的利润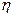 的分布列及数学期望
的分布列及数学期望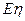
查看答案和解析>>
科目: 来源:2012届广西桂林中学高三7月月考试题理科数学 题型:解答题
(本题满分12分)某种家用电器每台的销售利润与该电器的无故障使用时间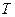 (单位:年)有关. 若
(单位:年)有关. 若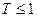 ,则销售利润为0元;若
,则销售利润为0元;若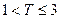 ,则销售利润为100元;若
,则销售利润为100元;若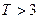 ,则销售利润为200元. 设每台该种电器的无故障使用时间
,则销售利润为200元. 设每台该种电器的无故障使用时间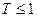 ,
,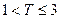 及
及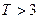 这三种情况发生的概率分别为
这三种情况发生的概率分别为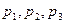 ,又知
,又知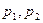 是方程
是方程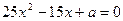 的两个根,且
的两个根,且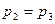 .
.
(Ⅰ)求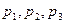 的值;
的值;
(Ⅱ)记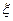 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求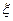 的分布列和期望。
的分布列和期望。
查看答案和解析>>
科目: 来源:2011届广东省高考猜押题卷文科数学(二)解析版 题型:解答题
(本小题满分12分)
新能源汽车是指除汽油、柴油发动机之外所有其它能源汽车.包括燃料电池汽车、混合动力汽车、氢能源动力汽车和太阳能汽车等.其废气排放量比较低.为了配合我国“节能减排”战略,某汽车厂决定转型生产新能源汽车中的燃料电池汽车、混合动力和氢能源动力三类轿车,每类轿车均有标准型和豪华型两种型号,某月的产量如下表(单位:辆):
| | 燃料电池轿车 | 混合动力轿车 | 氢能源动力轿车 |
| 标准型 | 100 | 200 |  |
| 豪华型 | 200 | 300 | 500 |
 的值.
的值. 查看答案和解析>>
科目: 来源:2010-2011年广东省广州市高二下学期期末教学质量检测理科数学 题型:解答题
(本小题满分14分)
广州市为了做好新一轮文明城市创建工作,有关部门为了解市民对《广州市创建全国文明城市小知识》的熟知程度,对下面两个问题进行了调查:
问题一:《广州市民“十不”行为规范》有哪“十不”?
问题二:广州市“一约三则”的内容是什么?
调查结果显示, 年龄段的市民回答第一个问题的正确率为
年龄段的市民回答第一个问题的正确率为 ,
, 年龄段的市民回答第二个问题正确率为
年龄段的市民回答第二个问题正确率为 .
.
为使活动得到市民更好的配合,调查单位采取如下激励措施:正确回答问题一者奖励价值20元的礼物;正确回答问题二奖励价值30元的礼物,有一家庭的两成员(大人42岁,孩子13岁)参与了此项活动,小孩回答第一个问题,大人回答第二个问题,问这个家庭获得礼物价值的数学期望是多少?
查看答案和解析>>
科目: 来源:2010-2011学年北京市东城区高二下学期期末考试理科数学 题型:解答题
(本小题满分7分)
有三张形状、大小、质地完全一致的卡片,在每张卡片上分别写上0,1,2,现从中任意抽取一张,将其上的数字记作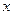 ,然后放回,再抽取一张,将其上的数字记作
,然后放回,再抽取一张,将其上的数字记作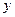 ,令
,令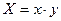 。
。
(Ⅰ)求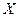 所取各值的概率;
所取各值的概率;
(Ⅱ)求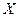 的分布列,并求出
的分布列,并求出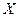 的数学期望值。
的数学期望值。
查看答案和解析>>
科目: 来源:2010-2011年北京市通州区高二下学期期末考试理科数学 题型:解答题
(本题10分)甲、乙、丙三名射击运动员射中目标的概率分别为 (0<a<1),三各射击一次,击中目标的次数记为
(0<a<1),三各射击一次,击中目标的次数记为 。
。
(Ⅰ)求 的分布列;
的分布列;
(Ⅱ)若 的值最大,求实数a的取值范围。
的值最大,求实数a的取值范围。
查看答案和解析>>
科目: 来源:2010-2011年北京市通州区高二下学期期末考试理科数学 题型:解答题
(本题8分)某果园要用三辆汽车将一批水果从所在城市E运至销售城市F,已知从城市E到城市F有两条公路。统计表明:汽车走公路Ⅰ堵车的概率为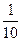 ,走公路Ⅱ堵车的概率为
,走公路Ⅱ堵车的概率为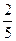 ,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响。
,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响。
(Ⅰ)求甲、乙两辆汽车中恰有一辆堵车的概率。
(Ⅱ)求三辆汽车中至少有两辆堵车的概率。
查看答案和解析>>
科目: 来源:2010-2011年北京市通州区高二下学期期末考试理科数学 题型:解答题
(本题8分)甲、乙、丙三人独立完 成某项任务的概率分别为
成某项任务的概率分别为 。且他们是否完成任务互不影响。
。且他们是否完成任务互不影响。
(Ⅰ)若 ,设甲、乙、丙三人中能完成任务人数为X,求X的分布列和数学期望EX;
,设甲、乙、丙三人中能完成任务人数为X,求X的分布列和数学期望EX;
(Ⅱ)若三人中只有丙完成了任务的概率为 ,求
,求 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com