
科目: 来源:2013-2014学年重庆市五区高三学业调研抽测1理科数学试卷(解析版) 题型:填空题
在直角坐标系 中,以原点
中,以原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.若点
轴的正半轴为极轴建立极坐标系.若点 为直线
为直线 上一点,点
上一点,点 为曲线
为曲线 为参数)上一点,则
为参数)上一点,则 的最小值为 .
的最小值为 .
查看答案和解析>>
科目: 来源:2013-2014学年重庆市五区高三学业调研抽测1理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(Ⅰ)若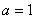 ,求函数
,求函数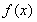 的单调区间和极值;
的单调区间和极值;
(Ⅱ)设函数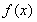 图象上任意一点的切线
图象上任意一点的切线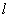 的斜率为
的斜率为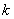 ,当
,当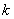 的最小值为1时,求此时切线
的最小值为1时,求此时切线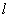 的方程.
的方程.
查看答案和解析>>
科目: 来源:2013-2014学年重庆市五区高三学业调研抽测1理科数学试卷(解析版) 题型:解答题
为了参加2013年市级高中篮球比赛,该市的某区决定从四所高中学校选出 人组成男子篮球队代表所在区参赛,队员来源人数如下表:
人组成男子篮球队代表所在区参赛,队员来源人数如下表:
学校 | 学校甲 | 学校乙 | 学校丙 | 学校丁 |
人数 |
|
|
|
|
该区篮球队经过奋力拼搏获得冠军,现要从中选出两名队员代表冠军队发言.
(Ⅰ)求这两名队员来自同一学校的概率;
(Ⅱ)设选出的两名队员中来自学校甲的人数为 ,求随机变量
,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目: 来源:2013-2014学年重庆市五区高三学业调研抽测1理科数学试卷(解析版) 题型:解答题
设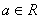 ,函数
,函数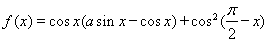 满足
满足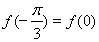 .
.
(Ⅰ)求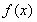 的单调递减区间;
的单调递减区间;
(Ⅱ)设锐角△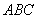 的内角
的内角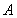 、
、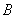 、
、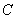 所对的边分别为
所对的边分别为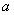 、
、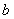 、
、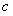 ,且
,且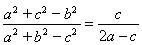 , 求
, 求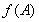 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2013-2014学年重庆市五区高三学业调研抽测1理科数学试卷(解析版) 题型:解答题
已知数列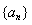 的前
的前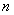 项和为
项和为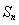 ,且
,且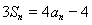 .
.
(Ⅰ)求数列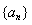 的通项公式;
的通项公式;
(Ⅱ)设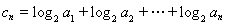 ,
,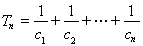 ,求使
,求使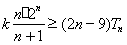 恒成立的实数
恒成立的实数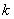 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2013-2014学年重庆市五区高三学业调研抽测1理科数学试卷(解析版) 题型:解答题
已知椭圆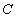 :
: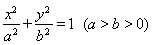 的左、右焦点分别为
的左、右焦点分别为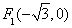 、
、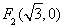 ,椭圆上的点
,椭圆上的点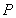 满足
满足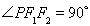 ,且△
,且△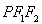 的面积为
的面积为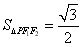 .
.
(Ⅰ)求椭圆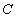 的方程;
的方程;
(Ⅱ)设椭圆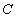 的左、右顶点分别为
的左、右顶点分别为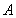 、
、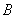 ,过点
,过点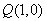 的动直线
的动直线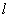 与椭圆
与椭圆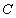 相交于
相交于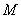 、
、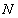 两点,直线
两点,直线 与直线
与直线 的交点为
的交点为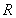 ,证明:点
,证明:点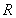 总在直线
总在直线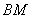 上.
上.
查看答案和解析>>
科目: 来源:2013-2014学年重庆市五区高三学业调研抽测1理科数学试卷(解析版) 题型:解答题
已知函数
 .
.
(Ⅰ)若函数 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)当 且
且 时,证明:
时,证明:  .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com