
科目: 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:选择题
已知正方形OABC的四个顶点O(0,0),A(1,0),B(1,1),C(0,1),设u=2xy,v=x2-y2,是一个由平面xOy到平面uOv上的变换,则正方形OABC在这个变换下的图形是( )
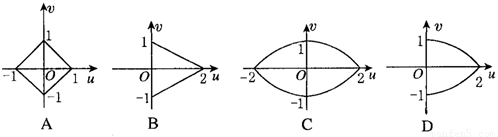
查看答案和解析>>
科目: 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:填空题
如图是容量为200的样本的频率分布直方图,则样本数据落在[10,14]内的频数为 。

查看答案和解析>>
科目: 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:填空题
函数f(x)=2+logax(a>0, a≠1)的图像恒过定点A,若点A在直线mx+ny-3=0上,其中mn>0,则 的最小值为
。
的最小值为
。
查看答案和解析>>
科目: 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:填空题
设a∈{1,2,3},b∈{2,4,6},则函数y= 是减函数的概率为 。
是减函数的概率为 。
查看答案和解析>>
科目: 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:填空题
过椭圆C: 的左顶点A且斜率为k的直线交椭圆C于另一个点B,且点B在x轴上的射影恰好为右焦点F,若
的左顶点A且斜率为k的直线交椭圆C于另一个点B,且点B在x轴上的射影恰好为右焦点F,若 <k<
<k< ,则椭圆的离心率的取值范围是
。
,则椭圆的离心率的取值范围是
。
查看答案和解析>>
科目: 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:填空题
定义在R上的函数f(x)及其导函数f'(x)的图像都是连续不断的曲线,且对于实数a, b (a<b)有f'(a)>0,f'(b)<0,现给出如下结论:
①$x0∈[a,b],f(x0)=0;②$x0∈[a,b],f(x0)>f(b);
③"x0∈[a,b],f(x0)>f(a);④$x0∈[a,b],f(a)-f(b)>f' x0)(a-b).
其中结论正确的有 。
查看答案和解析>>
科目: 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:解答题
在△ABC中,角A,B,C所对的边分别为a,b,c,且1+ =
= .
.
(Ⅰ)求角A;
(Ⅱ)已知 ,求
,求 的值。
的值。
查看答案和解析>>
科目: 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:解答题
某园艺师用两种不同的方法培育了一批珍贵树苗,在树苗3个月大的时候,随机抽取甲、乙两种方法培育的树苗各10株,测量其高度,得到的茎叶图如图所示(单位:cm).

(Ⅰ)依茎叶图判断用哪种方法培育的树苗的平均高度大?
(Ⅱ)现从用两种方法培育的高度不低于80cm的树苗中随机抽取两株,求至少有一株是甲方法培育的概率。
查看答案和解析>>
科目: 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:解答题
如图所示,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点。

(Ⅰ)求证:平面FGH⊥平面AEB;
(Ⅱ)在线段PC上是否存在一点M,使PB⊥平面EFM?若存在,求出线段PM的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:解答题
已知函数f(x)=x2-(a-1)x-b-1,当x∈[b, a]时,函数f(x)的图像关于y轴对称,数列 的前n项和为Sn,且Sn=f(n).
的前n项和为Sn,且Sn=f(n).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,Tn=b1+b2++bn,若Tn>2m,求m的取值范围。
,Tn=b1+b2++bn,若Tn>2m,求m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com