设双曲线的两个焦点为，P是双曲线上的一点，且,则△PF₁ F₂的面积等于(      )

A.10　　B.8　 C.8 　D. 16

已知矩形ABCD的顶点都在半径为5的球O的球面上，且AB＝6, BC=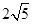，则棱锥O-ABCD的侧面积为(    )

A. 20+8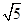　 B. 44 　　C、20　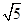　 D、46

偶函数满足，且在［0,1］时，，若直线kx－y＋k＝0(k>0)与函数的图象有且仅有三个交点，则k的取值范围是（    ）

A．   B．   C．   D．

已知函数，若，则           .

某三棱锥的三视图如图所示．则该三棱锥的体积为          ．

将1，2，3，4，5五个数字任意排成一排，且要求1和2相邻，则能排成五位偶数的概率

为              .

已知数列{｝的前n项和为，且，则使不等式成立的n的最大值为            ．

已知△ABC的三个内角A、B、C所对的边分别为a，b，c，且.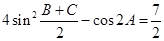

(1)求角A的大小，

(2)若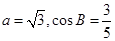，求△ABC的面积．

甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为，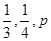

且他们是否破译出密码互不影响，若三人中只有甲破译出密码的概率为.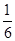

（1）求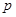的值，

 (2）设在甲、乙、丙三人中破译出密码的总人数为X，求X的分布列和数学期望E（X）.

如图，四棱锥P-ABCD的底面ABCD是正方形，PD⊥平面ABCD，E为PB上的点，且2BE=EP.

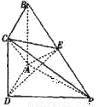
 (1）证明：AC⊥DE;

（2）若PC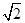＝BC，求二面角E－AC一P的余弦值.