
科目: 来源:2012-2013学年安徽省淮南二中高三(上)第三次月考数学试卷(理科)(解析版) 题型:选择题
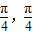 ]上是增函数; ④f(x)的图象关于直线x=
]上是增函数; ④f(x)的图象关于直线x=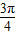 对称;
对称;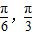 时,f(x)的值域为[-
时,f(x)的值域为[-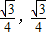 ].
].查看答案和解析>>
科目: 来源:2012-2013学年安徽省淮南二中高三(上)第三次月考数学试卷(理科)(解析版) 题型:选择题

 m
m m
m查看答案和解析>>
科目: 来源:2012-2013学年安徽省淮南二中高三(上)第三次月考数学试卷(理科)(解析版) 题型:选择题
 ,又存在互不相同的α,β,γ满足:f(α)=f(β)=f(γ),则αβγ的取值范围是( )
,又存在互不相同的α,β,γ满足:f(α)=f(β)=f(γ),则αβγ的取值范围是( )查看答案和解析>>
科目: 来源:2012-2013学年安徽省淮南二中高三(上)第三次月考数学试卷(理科)(解析版) 题型:选择题
 的值为( )
的值为( )

查看答案和解析>>
科目: 来源:2012-2013学年安徽省淮南二中高三(上)第三次月考数学试卷(理科)(解析版) 题型:选择题
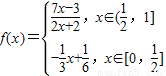 函数
函数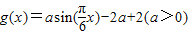 ,若存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是( )
,若存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是( )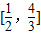
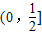
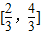
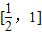
查看答案和解析>>
科目: 来源:2012-2013学年安徽省淮南二中高三(上)第三次月考数学试卷(理科)(解析版) 题型:填空题
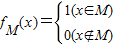 (其中M为非空数集且M?R),在实数集R上有两个非空真子集A、B满足A∩B=∅,则函数
(其中M为非空数集且M?R),在实数集R上有两个非空真子集A、B满足A∩B=∅,则函数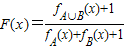 的值域为 .
的值域为 .查看答案和解析>>
科目: 来源:2012-2013学年安徽省淮南二中高三(上)第三次月考数学试卷(理科)(解析版) 题型:填空题
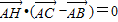 ;
;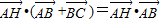 ;
;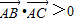 ,则△ABC为锐角三角形;
,则△ABC为锐角三角形;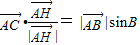 ;
;查看答案和解析>>
科目: 来源:2012-2013学年安徽省淮南二中高三(上)第三次月考数学试卷(理科)(解析版) 题型:填空题
 的函数因其图象类似于汉字“囧”字,故生动地称为“囧函数”,并把其与y轴的交点关于原点的对称点称为“囧点”,以“囧点”为圆心凡是与“囧函数”有公共点的圆,皆称之为“囧圆”,则当a=1,b=1时,所有的“囧圆”中,面积的最小值为 .
的函数因其图象类似于汉字“囧”字,故生动地称为“囧函数”,并把其与y轴的交点关于原点的对称点称为“囧点”,以“囧点”为圆心凡是与“囧函数”有公共点的圆,皆称之为“囧圆”,则当a=1,b=1时,所有的“囧圆”中,面积的最小值为 .查看答案和解析>>
科目: 来源:2012-2013学年安徽省淮南二中高三(上)第三次月考数学试卷(理科)(解析版) 题型:填空题
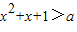 ,使命题P为真的实数a的取值范围为a<3;
,使命题P为真的实数a的取值范围为a<3; 的值与角a有关;
的值与角a有关; 的图象向左平移
的图象向左平移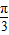 个单位长度后得到的图象所对应的函数是奇函数;
个单位长度后得到的图象所对应的函数是奇函数; 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com