相关习题
0 74701 74709 74715 74719 74725 74727 74731 74737 74739 74745 74751 74755 74757 74761 74767 74769 74775 74779 74781 74785 74787 74791 74793 74795 74796 74797 74799 74800 74801 74803 74805 74809 74811 74815 74817 74821 74827 74829 74835 74839 74841 74845 74851 74857 74859 74865 74869 74871 74877 74881 74887 74895 266669
科目:
来源:2012-2013学年湖北省黄冈市黄州区菱湖高中高一(上)期中数学试卷(解析版)
题型:填空题
已知m,n为直线,a,b为平面,给出下列结论:
①

⇒n∥a ②

⇒m∥n ③

⇒m∥n ④

⇒α∥β
其中正确结论的序号是:
.
查看答案和解析>>
科目:
来源:2012-2013学年湖北省黄冈市黄州区菱湖高中高一(上)期中数学试卷(解析版)
题型:填空题
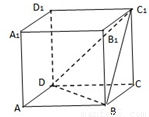
如图,在正方体ABCD-A
1B
1C
1D
1中,二面角C
1-BD-C的正切值为
.
查看答案和解析>>
科目:
来源:2012-2013学年湖北省黄冈市黄州区菱湖高中高一(上)期中数学试卷(解析版)
题型:填空题
①若a垂直于α内的两条相交直线,则a⊥α;
②若a垂直于α内的无数条直线,则a⊥α;
③若b∥β,则b平行于β内的所有直线;
④若a?α、b?β,a⊥b,则β⊥α;
⑤若a?α、b?β,β∥α,则a∥b;
⑥若b?β,b⊥α,则β⊥α;
其中正确的是 (只填序号)
查看答案和解析>>
科目:
来源:2012-2013学年湖北省黄冈市黄州区菱湖高中高一(上)期中数学试卷(解析版)
题型:填空题
如图,ABCD-A
1B
1C
1D
1为正方体,下面结论中正确的是
.
①AC∥平面CB
1D
1;
②AC
1⊥平面CB
1D
1;
③AC
1与底面ABCD所成角的正切值是

;
④AD
1与BD为异面直线.

查看答案和解析>>
科目:
来源:2012-2013学年湖北省黄冈市黄州区菱湖高中高一(上)期中数学试卷(解析版)
题型:解答题
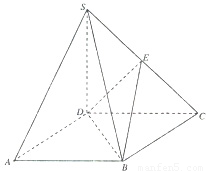
如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是平行四边形,∠BAD=30°,AB=2,AD=
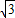
,E是SC的中点.
(Ⅰ)求证:SA∥平面BDE;
(Ⅱ)求证:AD⊥SB;
(Ⅲ)若SD=2,求二面角E-BD-C的余弦值.
查看答案和解析>>
科目:
来源:2012-2013学年湖北省黄冈市黄州区菱湖高中高一(上)期中数学试卷(解析版)
题型:解答题
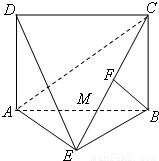
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
(1)求证:DE⊥BE;
(2)求四棱锥E-ABCD的体积;
(3)设点M在线段AB上,且AM=MB,试在线段CE上确定一点N,使得MN∥平面DAE.
查看答案和解析>>
科目:
来源:2012-2013学年湖北省黄冈市黄州区菱湖高中高一(上)期中数学试卷(解析版)
题型:解答题
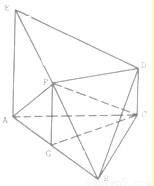
如图,几何体ABCD中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a,DC=a,F、G分别为EB何AB的中点.
(1)求证:FD∥平面ABC;
(2)求证:AF⊥BD;
(3)求二面角B-FC-G的正切值.
查看答案和解析>>
科目:
来源:2012-2013学年湖北省黄冈市黄州区菱湖高中高一(上)期中数学试卷(解析版)
题型:解答题
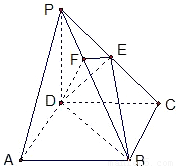
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
查看答案和解析>>
科目:
来源:2012-2013学年湖北省黄冈市黄州区菱湖高中高一(上)期中数学试卷(解析版)
题型:解答题
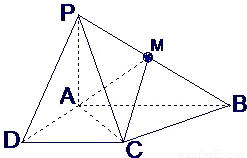
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=

AB=1,M是PB的中点.
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小.
查看答案和解析>>
科目:
来源:2012-2013学年湖北省黄冈市黄州区菱湖高中高一(上)期中数学试卷(解析版)
题型:解答题
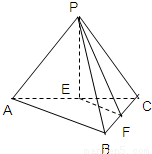
如图,在三棱锥P-ABC中,E,F分别为AC,BC的中点.
(1)求证:EF∥平面PAB;
(2)若平面PAC⊥平面ABC,且PA=PC,∠ABC=90°,求证:平面PEF⊥平面PBC.
查看答案和解析>>

 ⇒n∥a ②
⇒n∥a ② ⇒m∥n ③
⇒m∥n ③ ⇒m∥n ④
⇒m∥n ④ ⇒α∥β
⇒α∥β
 ;
;
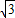 ,E是SC的中点.
,E是SC的中点.


 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC= AB=1,M是PB的中点.
AB=1,M是PB的中点.