相关习题
0 75192 75200 75206 75210 75216 75218 75222 75228 75230 75236 75242 75246 75248 75252 75258 75260 75266 75270 75272 75276 75278 75282 75284 75286 75287 75288 75290 75291 75292 75294 75296 75300 75302 75306 75308 75312 75318 75320 75326 75330 75332 75336 75342 75348 75350 75356 75360 75362 75368 75372 75378 75386 266669
科目:
来源:2012-2013学年湖北省鄂州二中高一(上)期中数学试卷(二)(解析版)
题型:填空题
函数f(x)=x2-2x+a在区间(-2,0)和(2,3)内各有一个零点,则实数a的取值范围是 .
查看答案和解析>>
科目:
来源:2012-2013学年湖北省鄂州二中高一(上)期中数学试卷(二)(解析版)
题型:填空题
定义min{f(x),g(x)}为f(x)与g(x)中的较小者,则函数min{2-x2,x}的最大值是 .
查看答案和解析>>
科目:
来源:2012-2013学年湖北省鄂州二中高一(上)期中数学试卷(二)(解析版)
题型:解答题
已知全集U=R,集合A={a|a≥2或a≤-2},B={a|关于x的方程ax2-x+1=0有实根},求A∪B,A∩B,A∪(∁UB).
查看答案和解析>>
科目:
来源:2012-2013学年湖北省鄂州二中高一(上)期中数学试卷(二)(解析版)
题型:解答题
已知函数f(x)=loga(x+1),g(x)=loga(4-2x)(a>0,且a≠1).
(Ⅰ)求函数f(x)+g(x)的定义域;
(Ⅱ)求使函数f(x)-g(x)的值为正数的x的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年湖北省鄂州二中高一(上)期中数学试卷(二)(解析版)
题型:解答题
已知函数
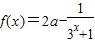
(a∈R).
(1)若函数f(x)为奇函数,求a的值;
(2)判断函数f(x)在R上的单调性,并证明.
查看答案和解析>>
科目:
来源:2012-2013学年湖北省鄂州二中高一(上)期中数学试卷(二)(解析版)
题型:解答题
已知二次函数f(x)满足条件f(0)=1,及f(x+1)-f(x)=2x.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[a,a+1](a∈R)上的最小值g(a)的表达式.
查看答案和解析>>
科目:
来源:2012-2013学年湖北省鄂州二中高一(上)期中数学试卷(二)(解析版)
题型:解答题
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
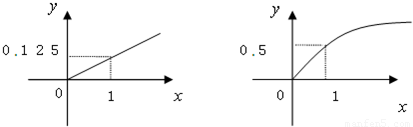
(1)分别写出两种产品的收益与投资的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?
查看答案和解析>>
科目:
来源:2012-2013学年湖北省鄂州二中高一(上)期中数学试卷(二)(解析版)
题型:解答题
已知函数f(x)定义在(-1,1)上,对于任意的x,y∈(-1,1),有f(x)+f(y)=f(
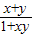
),且当x<0时,f(x)>0;
(1)验证函数f(x)=ln
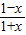
是否满足这些条件;
(2)判断这样的函数是否具有奇偶性和其单调性,并加以证明;
(3)若f(-

)=1,试解方程f(x)=-

.
查看答案和解析>>
科目:
来源:2012-2013学年辽宁省沈阳二中高一(上)期中数学试卷(解析版)
题型:选择题
设不等式x2-x≤0的解集为M,函数f(x)=ln(1-|x|)的定义域为N,则M∩N为( )
A.[0,1)
B.(0,1)
C.[0,1]
D.(-1,0]
查看答案和解析>>
科目:
来源:2012-2013学年辽宁省沈阳二中高一(上)期中数学试卷(解析版)
题型:选择题
若函数f(x)=x
3+x
2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
| f(1)=-2 | f(1.5)=0.625 |
| f(1.25)=-0.984 | f(1.375)=-0.260 |
| f(1.438)=0.165 | f(1.4065)=-0.052 |
那么方程x
3+x
2-2x-2=0的一个近似根(精确到0.1)为( )
A.1.2
B.1.3
C.1.4
D.1.5
查看答案和解析>>

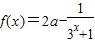 (a∈R).
(a∈R).
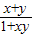 ),且当x<0时,f(x)>0;
),且当x<0时,f(x)>0;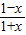 是否满足这些条件;
是否满足这些条件; )=1,试解方程f(x)=-
)=1,试解方程f(x)=- .
.