相关习题
0 75211 75219 75225 75229 75235 75237 75241 75247 75249 75255 75261 75265 75267 75271 75277 75279 75285 75289 75291 75295 75297 75301 75303 75305 75306 75307 75309 75310 75311 75313 75315 75319 75321 75325 75327 75331 75337 75339 75345 75349 75351 75355 75361 75367 75369 75375 75379 75381 75387 75391 75397 75405 266669
科目:
来源:2012-2013学年黑龙江省牡丹江一中高三(上)9月月考数学试卷(理科)(解析版)
题型:选择题
已知函数f(x)=lnx+a的导数为f′(x),若使得f′(x)=f(x)成立的x<1,则实数α的取值范围为( )
A.a>1
B.a<1
C.0<a<1
D.a≥1
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省牡丹江一中高三(上)9月月考数学试卷(理科)(解析版)
题型:选择题
已知函数f(x)=

,则下列关于函数y=f(f(x))+1的零点个数的判断正确的是( )
A.当a>0时,有4个零点;当a<0时,有1个零点
B.当a>0时,有3个零点;当a<0时,有2个零点
C.无论a为何值,均有2个零点
D.无论a为何值,均有4个零点
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省牡丹江一中高三(上)9月月考数学试卷(理科)(解析版)
题型:填空题
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省牡丹江一中高三(上)9月月考数学试卷(理科)(解析版)
题型:填空题
设函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图象过点(2,8),则a+b等于 .
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省牡丹江一中高三(上)9月月考数学试卷(理科)(解析版)
题型:填空题
下列四种说法中,
①命题“存在x∈R,x
2-x>0”的否定是“对于任意x∈R,x
2-x<0”;
②;命题“p且q为真”是“p或q为真”的必要不充分条件;
③已知幂函数f(x)=x
α的图象经过点(2,
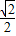
),则f(4)的值等于

④某路公共汽车每7分钟发车一次,某位乘客到乘车点的时刻是随机的,则他候车时间超过3分钟的概率是

.
说法正确的序号是
.
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省牡丹江一中高三(上)9月月考数学试卷(理科)(解析版)
题型:填空题
函数

且a≠1),存在实数m<n使不等式f(x)>0的解集为(m,n),则a的取值范围是
.
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省牡丹江一中高三(上)9月月考数学试卷(理科)(解析版)
题型:解答题
设函数f(x)=|2x-2|+|x+3|.
(1)解不等式f(x)>6;
(2)若关于x的不等式f(x)≤|2a-1|的解集不是空集,试求a的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省牡丹江一中高三(上)9月月考数学试卷(理科)(解析版)
题型:解答题
已知在直角坐标系xoy中,直线l过点P(1,-5),且倾斜角为

,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,半径为4的圆C的圆心的极坐标为

.
(Ⅰ)写出直线l的参数方程和圆C的极坐标方程;
(Ⅱ)试判定直线l和圆C的位置关系.
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省牡丹江一中高三(上)9月月考数学试卷(理科)(解析版)
题型:解答题
已知函数
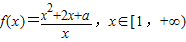
.
(Ⅰ)若对任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围;
(Ⅱ)若对任意a∈[-1,1],f(x)>4恒成立,求实数x的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省牡丹江一中高三(上)9月月考数学试卷(理科)(解析版)
题型:解答题
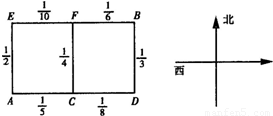
某人居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为

,路段CD发生堵车事件的概率为

)
(1)请你为其选择一条由A到B的最短路线(即此人只选择从西向东和从南向北的路线),使得途中发生堵车事件的概率最小;
(2)若记路线A→C→F→B中遇到堵车次数为随机变量ξ,求ξ的数学期望Eξ.
查看答案和解析>>

 ,则下列关于函数y=f(f(x))+1的零点个数的判断正确的是( )
,则下列关于函数y=f(f(x))+1的零点个数的判断正确的是( )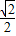 ),则f(4)的值等于
),则f(4)的值等于
 .
. 且a≠1),存在实数m<n使不等式f(x)>0的解集为(m,n),则a的取值范围是 .
且a≠1),存在实数m<n使不等式f(x)>0的解集为(m,n),则a的取值范围是 . ,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,半径为4的圆C的圆心的极坐标为
,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,半径为4的圆C的圆心的极坐标为 .
.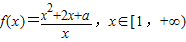 .
. ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为 )
)