相关习题
0 75469 75477 75483 75487 75493 75495 75499 75505 75507 75513 75519 75523 75525 75529 75535 75537 75543 75547 75549 75553 75555 75559 75561 75563 75564 75565 75567 75568 75569 75571 75573 75577 75579 75583 75585 75589 75595 75597 75603 75607 75609 75613 75619 75625 75627 75633 75637 75639 75645 75649 75655 75663 266669
科目:
来源:2012-2013学年江苏省阜宁中学、大丰中学联考高三(上)期中数学试卷(强化班)(解析版)
题型:填空题
已知函数

,设a,b∈R,且f(a)+f(b-1)=0,则a+b=
.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省阜宁中学、大丰中学联考高三(上)期中数学试卷(强化班)(解析版)
题型:填空题
查看答案和解析>>
科目:
来源:2012-2013学年江苏省阜宁中学、大丰中学联考高三(上)期中数学试卷(强化班)(解析版)
题型:填空题
已知数列{an}是首项为15、公差为整数的等差数列,前n项的和是Sn,S11≥0,S12<0,Sn的最大值是S,函数y=f(x)满足f(1+x)=f(5-x)对任意实数x都成立,且y=f(x) 的所有零点和恰好为S,则y=f(x)的零点的个数为 .
查看答案和解析>>
科目:
来源:2012-2013学年江苏省阜宁中学、大丰中学联考高三(上)期中数学试卷(强化班)(解析版)
题型:填空题
已知f(x)=x3-3x,过A(1,m)可作曲线y=f(x)的三条切线,则m的取值范围是 .
查看答案和解析>>
科目:
来源:2012-2013学年江苏省阜宁中学、大丰中学联考高三(上)期中数学试卷(强化班)(解析版)
题型:解答题
已知△ABC的三个内角A,B,C对应的边长分别为a,b,c,向量
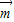
=(sinB,1-cosB)与向量
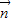
=(2,0)的夹角θ的余弦值为

.
(1)求角B的大小;
(2)若
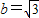
,求a+c的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省阜宁中学、大丰中学联考高三(上)期中数学试卷(强化班)(解析版)
题型:解答题
如图①,E,F分别是直角三角形ABC边AB和AC的中点,∠B=90°,沿EF将三角形ABC折成如图②所示的锐二面角A
1-EF-B,若M为线段A
1C中点.
求证:(1)直线FM∥平面A
1EB;
(2)平面A
1FC⊥平面A
1BC.

查看答案和解析>>
科目:
来源:2012-2013学年江苏省阜宁中学、大丰中学联考高三(上)期中数学试卷(强化班)(解析版)
题型:解答题
已知椭圆

(a>b>0)的两准线间距离为6,离心率

.过椭圆上任意一点P,作右准线的垂线PH(H为垂足),并延长PH到Q,使得

.F
2为该椭圆的右焦点,设点P的坐标为(x
,y
).
(1)求椭圆方程;
(2)当点P在椭圆上运动时,求λ的值使得点Q的轨迹是一个定圆.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省阜宁中学、大丰中学联考高三(上)期中数学试卷(强化班)(解析版)
题型:解答题
在一次数学实践活动课上,老师给一个活动小组安排了这样的一个任务:设计一个方案,将一块边长为4米的正方形铁片,通过裁剪、拼接的方式,将它焊接成容积至少有5立方米的长方体无盖容器(只有一个下底面和侧面的长方体).该活动小组接到任务后,立刻设计了一个方案,如下图所示,按图1在正方形铁片的四角裁去四个相同的小正方形后,将剩下的部分焊接成长方体(如图2).请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积,最大容积是多少?是否符合要求?若不符合,请你帮他们再设计一个能符合要求的方案,简单说明操作过程和理由.
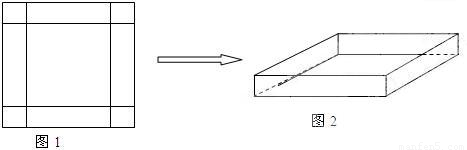
查看答案和解析>>
科目:
来源:2012-2013学年江苏省阜宁中学、大丰中学联考高三(上)期中数学试卷(强化班)(解析版)
题型:解答题
各项均为正数的数列{a
n}的前n项和为S
n,
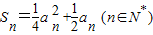
;
(1)求a
n;
(2)令
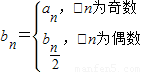
,
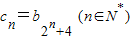
,求{c
n}的前n项和T
n;
(3)令
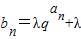
(λ、q为常数,q>0且q≠1),c
n=3+n+(b
1+b
2+…+b
n),是否存在实数对(λ、q),使得数列{c
n}成等比数列?若存在,求出实数对(λ、q)及数列{c
n}的通项公式,若不存在,请说明理由.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省阜宁中学、大丰中学联考高三(上)期中数学试卷(强化班)(解析版)
题型:解答题
已知函数f(x)=alnx+x2(a为实常数).
(1)若a=-2,求证:函数f(x)在(1,+∞)上是增函数;
(2)求函数f(x)在[1,e]上的最小值及相应的x值;
(3)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.
查看答案和解析>>

 ,设a,b∈R,且f(a)+f(b-1)=0,则a+b= .
,设a,b∈R,且f(a)+f(b-1)=0,则a+b= .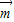 =(sinB,1-cosB)与向量
=(sinB,1-cosB)与向量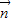 =(2,0)的夹角θ的余弦值为
=(2,0)的夹角θ的余弦值为 .
.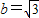 ,求a+c的取值范围.
,求a+c的取值范围.
 (a>b>0)的两准线间距离为6,离心率
(a>b>0)的两准线间距离为6,离心率 .过椭圆上任意一点P,作右准线的垂线PH(H为垂足),并延长PH到Q,使得
.过椭圆上任意一点P,作右准线的垂线PH(H为垂足),并延长PH到Q,使得 .F2为该椭圆的右焦点,设点P的坐标为(x,y).
.F2为该椭圆的右焦点,设点P的坐标为(x,y).
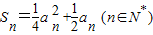 ;
;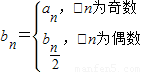 ,
,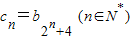 ,求{cn}的前n项和Tn;
,求{cn}的前n项和Tn;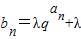 (λ、q为常数,q>0且q≠1),cn=3+n+(b1+b2+…+bn),是否存在实数对(λ、q),使得数列{cn}成等比数列?若存在,求出实数对(λ、q)及数列{cn}的通项公式,若不存在,请说明理由.
(λ、q为常数,q>0且q≠1),cn=3+n+(b1+b2+…+bn),是否存在实数对(λ、q),使得数列{cn}成等比数列?若存在,求出实数对(λ、q)及数列{cn}的通项公式,若不存在,请说明理由.