相关习题
0 75624 75632 75638 75642 75648 75650 75654 75660 75662 75668 75674 75678 75680 75684 75690 75692 75698 75702 75704 75708 75710 75714 75716 75718 75719 75720 75722 75723 75724 75726 75728 75732 75734 75738 75740 75744 75750 75752 75758 75762 75764 75768 75774 75780 75782 75788 75792 75794 75800 75804 75810 75818 266669
科目:
来源:2012-2013学年湖南省衡阳八中高三(上)第二次月考试卷试卷(理科)(解析版)
题型:填空题
在各项均为负数的数列{a
n}中,已知点
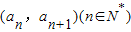
在函数
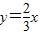
的图象上,且
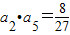
.则数列{a
n}的通项公式为a
n=
.
查看答案和解析>>
科目:
来源:2012-2013学年湖南省衡阳八中高三(上)第二次月考试卷试卷(理科)(解析版)
题型:填空题
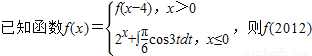
=
.
查看答案和解析>>
科目:
来源:2012-2013学年湖南省衡阳八中高三(上)第二次月考试卷试卷(理科)(解析版)
题型:填空题
某学生对函数f(x)=2x•cosx的性质进行研究,得出如下的结论:
①点(0,0)是函数y=f(x)图象的一个对称中心;
②函数y=f(x)图象关于y轴对称;
③函数f(x)在[-π,0]上单调递增,在[0,π]上也单调递增;
④存在常数M>0,使|f(x)|≤M|x|对一切实数x均成立.
其中正确的结论是 .
查看答案和解析>>
科目:
来源:2012-2013学年湖南省衡阳八中高三(上)第二次月考试卷试卷(理科)(解析版)
题型:填空题
设函数f(x)的定义域为D,若存在非零实数t,使得对于任意x∈M(M⊆D)有x+t∈D且f(x+t)≥f(x),则称f(x)在M上的t给力函数,若定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上的m给力函数,则m的取值范围为 .
查看答案和解析>>
科目:
来源:2012-2013学年湖南省衡阳八中高三(上)第二次月考试卷试卷(理科)(解析版)
题型:解答题
已知向量
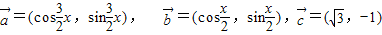
,其中x∈R,
(1)当
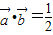
时,求x值的集合;
(2)设函数
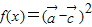
,求f(x)的最小正周期及其单调增区间.
查看答案和解析>>
科目:
来源:2012-2013学年湖南省衡阳八中高三(上)第二次月考试卷试卷(理科)(解析版)
题型:解答题
△ABC中,a,b,c分别是角A、B、C的对边,向量
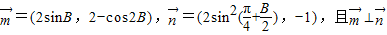
.
(1)求角B的大小;
(2)若a=
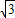
,b=1,求c的值.
查看答案和解析>>
科目:
来源:2012-2013学年湖南省衡阳八中高三(上)第二次月考试卷试卷(理科)(解析版)
题型:解答题
已知数列{a
n}满足:1•a
1+2•a
2+3•a
3+…n•a
n=n
(1)求{a
n}的通项公式;
(2)若
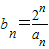
,求{b
n}的前n项和S
n.
查看答案和解析>>
科目:
来源:2012-2013学年湖南省衡阳八中高三(上)第二次月考试卷试卷(理科)(解析版)
题型:解答题
已知函数f(x)=lnx,g(x)=(m+1)x2-x(m≠-1).
(1)求f(x)在x=1处的切线方程;
(2)若函数y=f(x)与y=g(x)的图象有公共点,且在公共点P处有相同的切线,求实数m的值和P的坐标.
查看答案和解析>>
科目:
来源:2012-2013学年湖南省衡阳八中高三(上)第二次月考试卷试卷(理科)(解析版)
题型:解答题
已知数列{a
n}的前n项为和S
n,点
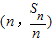
在直线
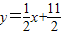
上.数列{b
n}满足b
n+2-2b
n+1+b
n=0(n∈N
*),且b
3=11,前9项和为153.
(Ⅰ)求数列{a
n}、{b
n}的通项公式;
(Ⅱ)设
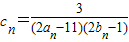
,数列{c
n}的前n和为T
n,求使不等式
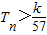
对一切n∈N
*都成立的最大正整数k的值.
(Ⅲ)设
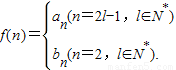
是否存在m∈N
*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:2012-2013学年湖南省衡阳八中高三(上)第二次月考试卷试卷(理科)(解析版)
题型:解答题
设f(x)是定义在区间(1,+∞)上的函数,其导函数为f'(x).如果存在实数a和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得f'(x)=h(x)(x
2-ax+1),则称函数f(x)具有性质P(a).
(1)设函数

,其中b为实数.
(i)求证:函数f(x)具有性质P(b);
(ii)求函数f(x)的单调区间.
(2)已知函数g(x)具有性质P(2),给定x
1,x
2∈(1,+∞),x
1<x
2,设m为实数,a=mx
1+(1-m)x
2,β=(1-m)x
1+mx
2,且a>1,β>1,若|g(a)-g(β)|<|g(x
1)-g(x
2)|,求m取值范围.
查看答案和解析>>

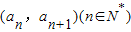 在函数
在函数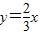 的图象上,且
的图象上,且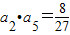 .则数列{an}的通项公式为an= .
.则数列{an}的通项公式为an= .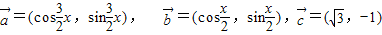 ,其中x∈R,
,其中x∈R,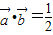 时,求x值的集合;
时,求x值的集合;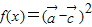 ,求f(x)的最小正周期及其单调增区间.
,求f(x)的最小正周期及其单调增区间.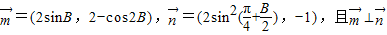 .
.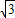 ,b=1,求c的值.
,b=1,求c的值.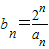 ,求{bn}的前n项和Sn.
,求{bn}的前n项和Sn.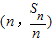 在直线
在直线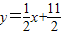 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.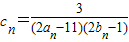 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式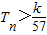 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.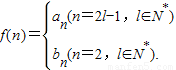 是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由. ,其中b为实数.
,其中b为实数.