
科目: 来源:2012-2013学年辽宁省五校协作体高三(上)联合竞赛数学试卷(理科)(解析版) 题型:选择题
 的零点按从小到大的顺序排列成一个数列,则该数列的前n项的和为Sn,则S10=( )
的零点按从小到大的顺序排列成一个数列,则该数列的前n项的和为Sn,则S10=( )
查看答案和解析>>
科目: 来源:2012-2013学年辽宁省五校协作体高三(上)联合竞赛数学试卷(理科)(解析版) 题型:填空题
 >2;
>2; 的取值范围为(-∞,-
的取值范围为(-∞,- )∪(
)∪( ,+∞).
,+∞).查看答案和解析>>
科目: 来源:2012-2013学年辽宁省五校协作体高三(上)联合竞赛数学试卷(理科)(解析版) 题型:填空题
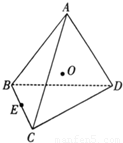
查看答案和解析>>
科目: 来源:2012-2013学年辽宁省五校协作体高三(上)联合竞赛数学试卷(理科)(解析版) 题型:解答题
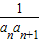 }的前n项和为Mn,求证:
}的前n项和为Mn,求证: ≤Mn<
≤Mn< .
.查看答案和解析>>
科目: 来源:2012-2013学年辽宁省五校协作体高三(上)联合竞赛数学试卷(理科)(解析版) 题型:解答题
| 指针位置 | A区域 | B区域 | C区域 |
| 返存金额(单位:元) | 60 | 30 |
 ,标准差
,标准差 ,求n、p的值;
,求n、p的值;
查看答案和解析>>
科目: 来源:2012-2013学年辽宁省五校协作体高三(上)联合竞赛数学试卷(理科)(解析版) 题型:解答题
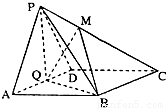
查看答案和解析>>
科目: 来源:2012-2013学年辽宁省五校协作体高三(上)联合竞赛数学试卷(理科)(解析版) 题型:解答题
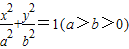 的两焦点,与椭圆有且仅有两个公共点:直线y=kx+m与圆x2+y2=1相切,与椭圆
的两焦点,与椭圆有且仅有两个公共点:直线y=kx+m与圆x2+y2=1相切,与椭圆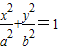 相交于A,B两点记
相交于A,B两点记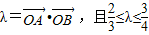 .
.查看答案和解析>>
科目: 来源:2012-2013学年辽宁省五校协作体高三(上)联合竞赛数学试卷(理科)(解析版) 题型:解答题
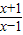 ,求函数φ(x)的单调区间;
,求函数φ(x)的单调区间;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com