相关习题
0 75689 75697 75703 75707 75713 75715 75719 75725 75727 75733 75739 75743 75745 75749 75755 75757 75763 75767 75769 75773 75775 75779 75781 75783 75784 75785 75787 75788 75789 75791 75793 75797 75799 75803 75805 75809 75815 75817 75823 75827 75829 75833 75839 75845 75847 75853 75857 75859 75865 75869 75875 75883 266669
科目:
来源:2012-2013学年四川省成都外国语学校AP国际部高二(上)期末数学试卷(解析版)
题型:填空题
给出下列四个命题
(1)“k=1”是“函数y=cos
2kx-sin
2kx的最小正周期为π”的充要条件;
(2)“a=3”是“直线ax+2y+3a=0与直线3x+(a-1)y=a-7互相平行”的充要条件;
(3)函数

的最小值为2;
(4)双曲线

的两条渐近线是

.
其中是假命题为
(将你认为是假命题的序号都填上)
查看答案和解析>>
科目:
来源:2012-2013学年四川省成都外国语学校AP国际部高二(上)期末数学试卷(解析版)
题型:解答题
已知点B是曲线2x2+1-y=0上任意一点,A(0,4)且M是线段AB中点,求动点M的轨迹方程.
查看答案和解析>>
科目:
来源:2012-2013学年四川省成都外国语学校AP国际部高二(上)期末数学试卷(解析版)
题型:解答题
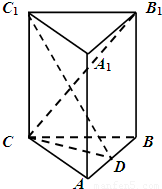
在三棱柱ABC-A
1B
1C
1中,CC
1垂直平面ABC,三角形ABC为等边三角形,D为AB中点.
(1)求证:AB⊥C
1D;
(2)求证:AC
1∥平面CDB
1.
(3)如果AB=4cm,AA
1=
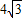
cm,求异面直线C
1D与AA
1所成角的大小.
查看答案和解析>>
科目:
来源:2012-2013学年四川省成都外国语学校AP国际部高二(上)期末数学试卷(解析版)
题型:解答题
已知双曲线4x
2-y
2=1及直线y=x+m.
(1)当m为何值时,直线与双曲线有公共点?
(2)若直线被双曲线截得的弦长为
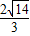
,求直线的方程.
查看答案和解析>>
科目:
来源:2012-2013学年四川省成都外国语学校AP国际部高二(上)期末数学试卷(解析版)
题型:解答题
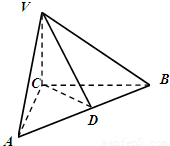
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=2,
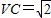
.
(1)求证:平面VAB⊥平面VCD;
(2)求二面角V-AB-C的大小;
(3)求点C到平面VAB的距离.
查看答案和解析>>
科目:
来源:2012-2013学年四川省成都外国语学校AP国际部高二(上)期末数学试卷(解析版)
题型:解答题
已知椭圆E:
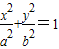
(a>b>0)过点P(3,1),其左、右焦点分别为F
1,F
2,且
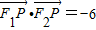
.
(1)求椭圆E的方程;
(2)若M,N是直线x=5上的两个动点,且F
1M⊥F
2N,则以MN为直径的圆C是否过定点?请说明理由.
查看答案和解析>>
科目:
来源:2012-2013学年贵州省安顺学院附中高二(上)期中数学试卷(理科)(解析版)
题型:选择题
下列不等式,正确的是( )
A.若a>b>0,c<0,则
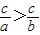
.
B.若a>b>0,c>d,则ac>bd.
C.若a>b,c>d,则a-c<b-d.
D.若a>b,ab>0,则
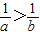
.
查看答案和解析>>
科目:
来源:2012-2013学年贵州省安顺学院附中高二(上)期中数学试卷(理科)(解析版)
题型:选择题
如图是一个正方体盒子的平面展开图,在其中的两个正方形内标有数字1、2、3,要在其余正方形内分别填上-1、-2、-3,使得按虚线折成正方体后,相对面上的两数互为相反数,则A处应填( )
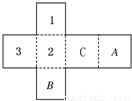
A.-2
B.-1
C.-3
D.-3、-2、-1均可
查看答案和解析>>
科目:
来源:2012-2013学年贵州省安顺学院附中高二(上)期中数学试卷(理科)(解析版)
题型:选择题
下列说法正确的是( )
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥
D.棱台各侧棱的延长线交于一点
查看答案和解析>>
科目:
来源:2012-2013学年贵州省安顺学院附中高二(上)期中数学试卷(理科)(解析版)
题型:选择题
设α、β是两个不同的平面,l、m是两条不重合的直线,下列命题中正确的是( )
A.若l∥α,α∩β=m,则l∥m
B.若l∥m,m?α,则l∥α
C.若l∥α,m∥β且α∥β,则l∥m
D.若l⊥α,m⊥β且α⊥β,则l⊥m
查看答案和解析>>

 的最小值为2;
的最小值为2; 的两条渐近线是
的两条渐近线是 .
.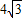 cm,求异面直线C1D与AA1所成角的大小.
cm,求异面直线C1D与AA1所成角的大小.
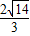 ,求直线的方程.
,求直线的方程.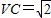 .
.
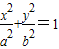 (a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且
(a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且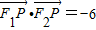 .
.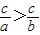 .
.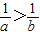 .
.