相关习题
0 76118 76126 76132 76136 76142 76144 76148 76154 76156 76162 76168 76172 76174 76178 76184 76186 76192 76196 76198 76202 76204 76208 76210 76212 76213 76214 76216 76217 76218 76220 76222 76226 76228 76232 76234 76238 76244 76246 76252 76256 76258 76262 76268 76274 76276 76282 76286 76288 76294 76298 76304 76312 266669
科目:
来源:2012-2013学年北京39中高三(上)期中数学试卷(文科)(解析版)
题型:填空题
一个几何体的三视图如图所示,则该几何体的表面积为
.
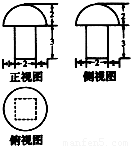
查看答案和解析>>
科目:
来源:2012-2013学年北京39中高三(上)期中数学试卷(文科)(解析版)
题型:填空题
2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cos2θ的值等于
.
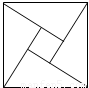
查看答案和解析>>
科目:
来源:2012-2013学年北京39中高三(上)期中数学试卷(文科)(解析版)
题型:填空题

如图,已知△ABC和△BCD所在平面互相垂直,∠ABC=∠BCD=90°,AB=a,BC=b,CD=c,且a
2+b
2+c
2=1,则三棱锥A-BCD的外接球的表面积为
.
查看答案和解析>>
科目:
来源:2012-2013学年北京39中高三(上)期中数学试卷(文科)(解析版)
题型:解答题
△ABC中,角A、B、C所对边分别是
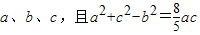
.
(1)求cos(A+C)+sin2B的值;
(2)若b=2,求△ABC面积的最大值.
查看答案和解析>>
科目:
来源:2012-2013学年北京39中高三(上)期中数学试卷(文科)(解析版)
题型:解答题
已知向量
=(sin x,cos x),
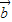
=(sin x,sin x),
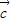
=(-1,0).
(1)若x=
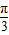
,求向量
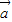
与
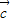
的夹角θ;
(2)若x∈[
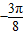
,
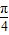
],求函数f(x)=
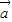
•
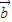
的最值;
(3)函数f(x)的图象可以由函数y=
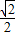
sin 2x (x∈R)的图象经过怎样的变换得到?
查看答案和解析>>
科目:
来源:2012-2013学年北京39中高三(上)期中数学试卷(文科)(解析版)
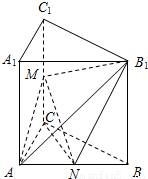
题型:解答题
如图,已知三棱柱ABC-A
1B
1C
1中,AA
1⊥底面ABC,AC=BC=2,AA
1=4,
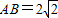
,M,N分别是棱CC
1,AB中点.
(Ⅰ)求证:CN⊥平面ABB
1A
1;
(Ⅱ)求证:CN∥平面AMB
1;
(Ⅲ)求三棱锥B
1-AMN的体积.
查看答案和解析>>
科目:
来源:2012-2013学年北京39中高三(上)期中数学试卷(文科)(解析版)
题型:解答题
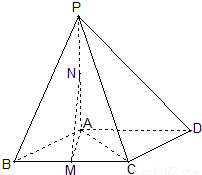
如图在四棱锥P-ABCD中底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点M、N分别是BC、PA的中点,且PA=AB=2
(1)证明:平面PBC⊥平面AMN;
(2)在线段PD上是否存在一点E,使得NM∥平面ACE;若存在,求出PE的长;若不存在,说明理由.
查看答案和解析>>
科目:
来源:2012-2013学年北京39中高三(上)期中数学试卷(文科)(解析版)
题型:解答题
在直角坐标系xOy中
(1)以原点为圆心的圆O与直线
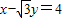
相切.求圆O的方程;
(2)从点A(4,4)引圆的切线,切点为B,求切线长|AB|的值;
(3)P(x,y)是圆O上任意一点,求 x-2y的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年北京39中高三(上)期中数学试卷(文科)(解析版)
题型:解答题
已知点M(-2,0),N(2,0),动点P满足条件
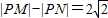
.记动点P的轨迹为W.
(1)求W的方程;
(2)若A,B是W上的不同两点,O是坐标原点,求
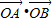
的最小值.
查看答案和解析>>
科目:
来源:2012-2013学年北京39中高三(上)期中数学试卷(文科)(解析版)
题型:解答题
在平面直角坐标系中,点集A={(x,y)|x2+y2≤1},B={(x,y)|x≤4,y≥0,3x-4y≥0},则
①点集P={(x,y)|x=x1+3,y=y1+1,(x1,y1)∈A}所表示的区域的面积为______;
②点集Q={(x,y)|x=x1+x2,y=y1+y2,(x1,y1)∈A,(x2,y2)∈B}所表示的区域的面积为______.
查看答案和解析>>


 如图,已知△ABC和△BCD所在平面互相垂直,∠ABC=∠BCD=90°,AB=a,BC=b,CD=c,且a2+b2+c2=1,则三棱锥A-BCD的外接球的表面积为 .
如图,已知△ABC和△BCD所在平面互相垂直,∠ABC=∠BCD=90°,AB=a,BC=b,CD=c,且a2+b2+c2=1,则三棱锥A-BCD的外接球的表面积为 .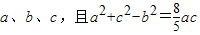 .
.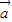 =(sin x,cos x),
=(sin x,cos x),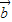 =(sin x,sin x),
=(sin x,sin x),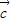 =(-1,0).
=(-1,0).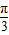 ,求向量
,求向量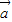 与
与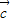 的夹角θ;
的夹角θ;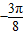 ,
,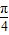 ],求函数f(x)=
],求函数f(x)=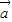 •
•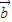 的最值;
的最值;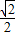 sin 2x (x∈R)的图象经过怎样的变换得到?
sin 2x (x∈R)的图象经过怎样的变换得到?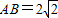 ,M,N分别是棱CC1,AB中点.
,M,N分别是棱CC1,AB中点.

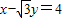 相切.求圆O的方程;
相切.求圆O的方程;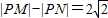 .记动点P的轨迹为W.
.记动点P的轨迹为W.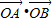 的最小值.
的最小值.