相关习题
0 76337 76345 76351 76355 76361 76363 76367 76373 76375 76381 76387 76391 76393 76397 76403 76405 76411 76415 76417 76421 76423 76427 76429 76431 76432 76433 76435 76436 76437 76439 76441 76445 76447 76451 76453 76457 76463 76465 76471 76475 76477 76481 76487 76493 76495 76501 76505 76507 76513 76517 76523 76531 266669
科目:
来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
在极坐标系xoy中,定点A(2,π),动点B在直线
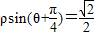
上运动,则线段AB的最短长度为
.
查看答案和解析>>
科目:
来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
若命题p:?x∈[1,3],x2-2ax+5>0是假命题,则实数a的取值范围是 .
查看答案和解析>>
科目:
来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D),有x+l∈D,且f(x+l)≥f(x),则称f(x)为M上的“l高调函数”.现给出下列命题:
①函数f(x)=2x为R上的“1高调函数”;
②函数f(x)=sin2x为R上的“A高调函数”;
③如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上“m高调函数”,那么实数m的取值范围是[2,+∞);
其中正确的命题是 .(写出所有正确命题的序号)
查看答案和解析>>
科目:
来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
已知函数

与函数g(x)的图象关于y=x对称,
(1)若g(a)g(b)=2,且a<0,b<0,则

的最大值为
(2)设f(x)是定义在R上的偶函数,对任意的x∈R,都有f(2-x)=f(x+2),且当x∈[-2,0]时,f(x)=g(x)-1,若关于x的方程f(x)-

=0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是
.
查看答案和解析>>
科目:
来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
已知集合A={x|(x-2)[x-(3a+1)]<0},集合B=
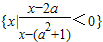
.
(1)当a=2时,求A∩B;
(2)当a
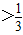
时,若元素x∈A是x∈B的必要条件,求实数a的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
设命题P:函数y=xc-1在(0,+∞)上为减函数,命题Q:y=ln(2cx2+2x+1)的值域为R,命题T:函数y=ln(2cx2+2x+1)定义域为R,
(1)若命题T为真命题,求c的取值范围.
(2)若P或Q为真命题,P且Q为假命题,求c的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
设函数f(x)是定义在(0,+∞)上的减函数,并且满足f(xy)=f(x)+f(y),f(

)=1,
(1)求f(1),f(

),f(9)的值,
(2)如果f(x)+f(2-x)<2,求x的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
设函数

(a,b为常数),且方程
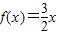
有两个实根为x
1=-1,x
2=2,
(1)求y=f(x)的解析式;
(2)证明:曲线y=f(x)的图象是一个中心对称图形,并求其对称中心.
查看答案和解析>>
科目:
来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
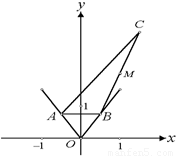
设A、B为函数
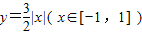
图象上不同的两个点,且 AB∥x轴,又有定点
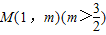
,已知M是线段BC的中点.
(1)设点B的横坐标为t,写出△ABC的面积S关于t的函数S=f(t)的表达式;
(2)求函数S=f(t)的最大值,并求此时点C的坐标.
查看答案和解析>>
科目:
来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
已知f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,当x∈(0,+∞)时,f(x)=ax+2lnx,(a∈R)
(1)求f(x)的解析式;
(2)是否存在负实数a,使得当x∈[-e,0)时,f(x)的最小值是4?如果存在,求出a的值;如果不存在,请说明理由.
(3)对x∈D如果函数F(x)的图象在函数G(x)的图象的下方,则称函数F(x)在D上被函数G(x)覆盖.求证:若a=1时,函数f(x)在区间x∈(1,+∞)上被函数g(x)=x3覆盖.
查看答案和解析>>

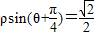 上运动,则线段AB的最短长度为 .
上运动,则线段AB的最短长度为 . 与函数g(x)的图象关于y=x对称,
与函数g(x)的图象关于y=x对称, 的最大值为
的最大值为  =0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
=0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .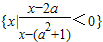 .
.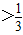 时,若元素x∈A是x∈B的必要条件,求实数a的取值范围.
时,若元素x∈A是x∈B的必要条件,求实数a的取值范围. )=1,
)=1, ),f(9)的值,
),f(9)的值, (a,b为常数),且方程
(a,b为常数),且方程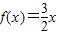 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2, 设A、B为函数
设A、B为函数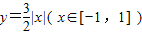 图象上不同的两个点,且 AB∥x轴,又有定点
图象上不同的两个点,且 AB∥x轴,又有定点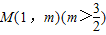 ,已知M是线段BC的中点.
,已知M是线段BC的中点.