相关习题
0 76495 76503 76509 76513 76519 76521 76525 76531 76533 76539 76545 76549 76551 76555 76561 76563 76569 76573 76575 76579 76581 76585 76587 76589 76590 76591 76593 76594 76595 76597 76599 76603 76605 76609 76611 76615 76621 76623 76629 76633 76635 76639 76645 76651 76653 76659 76663 76665 76671 76675 76681 76689 266669
科目:
来源:2012-2013学年浙江省金华市永康市明珠学校高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
设f(x)是定义在R上的奇函数,在(-∞,0)上有2xf′(2x)+f(2x)<0且f(-2)=0,则不等式xf(2x)<0的解集为 .
查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市永康市明珠学校高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
如图,矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC中点,K为△ADF的外心,沿EF将矩形折成一个120°的二面角A-EF-B,则此时KG的长是
.

查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市永康市明珠学校高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
给定正整数n(n≥2)按右图方式构成倒立三角形数表,第一行依次写上数l,2,3,…,n,在第一行的每相邻两个数正中间的下方写上这两个数之和,得到第二行的数(比上一行少一个数),依此类推,最后一行(第n行)只有一个数,例如n=6时数表如图所,则当n=2009时最后一行的数是
.

查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市永康市明珠学校高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
在△ABC中,A,B,C的对边分别为a,b,c,向量
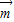
=(a,b),
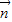
=(b,c).
(1)若向量
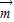
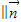
,求满足
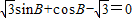
的角B的值;
(2)若

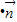
=2b
2,且A-C=
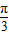
,求cosB的值.
查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市永康市明珠学校高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
数列{a
n}满足 a
n=2a
n-1+2
n+1(n∈N,n≥2),a
3=27.
(Ⅰ)求a
1,a
2的值;
(Ⅱ)记

,是否存在一个实数t,使数列{b
n}为等差数列?若存在,求出实数t;若不存在,请说明理由;
(Ⅲ)求数列{a
n}的前n项和S
n.
查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市永康市明珠学校高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
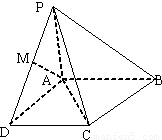
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,PA=
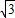
,∠ACB=90°,M是线段PD上的一点(不包括端点).
(Ⅰ)求证:BC⊥平面PAC;
(Ⅱ)求二面角D-PC-A的正切值;
(Ⅲ)试确定点M的位置,使直线MA与平面PCD所成角θ的正弦值为
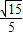
.
查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市永康市明珠学校高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
设f(x)=3ax
2+2bx+c(a≠0),若a+b+c=0,f(0)f(1)>0,求证:
(1)方程f(x)=0有实数根;
(2)-2<
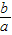
<-1;
(3)设x
1,x
2是方程f(x)=0的两个实数根,则
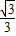
≤|x
1-x
2|
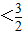
.
查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市永康市明珠学校高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
已知函数f (x)=e
g(x),g (x)=

(e是自然对数的底),
(1)若函数g (x)是(1,+∞)上的增函数,求k的取值范围;
(2)若对任意的x>0,都有f (x)<x+1,求满足条件的最大整数k的值;
(3)证明:ln(1+1×2)+ln(1+2×3)+…+ln[1+n (n+1)]>2n-3 (n∈N*).
查看答案和解析>>
科目:
来源:2012-2013学年贵州省遵义四中高三(上)第三次月考数学试卷(理科)(解析版)
题型:选择题
集合A={-1,0,1},A的子集中,含有元素0的子集共有( )
A.2个
B.4个
C.6个
D.8个
查看答案和解析>>
科目:
来源:2012-2013学年贵州省遵义四中高三(上)第三次月考数学试卷(理科)(解析版)
题型:选择题
查看答案和解析>>



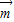 =(a,b),
=(a,b),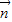 =(b,c).
=(b,c).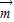
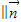 ,求满足
,求满足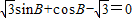 的角B的值;
的角B的值;
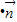 =2b2,且A-C=
=2b2,且A-C=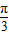 ,求cosB的值.
,求cosB的值. ,是否存在一个实数t,使数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;
,是否存在一个实数t,使数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;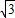 ,∠ACB=90°,M是线段PD上的一点(不包括端点).
,∠ACB=90°,M是线段PD上的一点(不包括端点).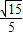 .
.
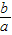 <-1;
<-1;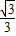 ≤|x1-x2|
≤|x1-x2|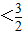 .
. (e是自然对数的底),
(e是自然对数的底),