相关习题
0 76585 76593 76599 76603 76609 76611 76615 76621 76623 76629 76635 76639 76641 76645 76651 76653 76659 76663 76665 76669 76671 76675 76677 76679 76680 76681 76683 76684 76685 76687 76689 76693 76695 76699 76701 76705 76711 76713 76719 76723 76725 76729 76735 76741 76743 76749 76753 76755 76761 76765 76771 76779 266669
科目:
来源:2012-2013学年云南省昆明一中高三(上)第一次月考数学试卷(文科)(解析版)
题型:选择题
如果执行如图的程序框图,则输出的结构是( )
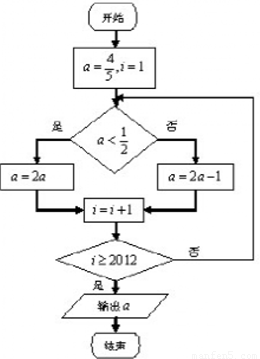
A.

B.

C.

D.

查看答案和解析>>
科目:
来源:2012-2013学年云南省昆明一中高三(上)第一次月考数学试卷(文科)(解析版)
题型:选择题
用[a]表示不大于实数a的最大整数,如[1.68]=1,设x1,x2分别是方程x+2x=3及x+log2(x-1)=3的根,则[x1+x2]=( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:
来源:2012-2013学年云南省昆明一中高三(上)第一次月考数学试卷(文科)(解析版)
题型:选择题
一个几何的三视图如图所示,它们都是腰长为1的等腰直角三角形,则该几何体的外接球的体积等于( )

A.

B.

C.π
D.2π
查看答案和解析>>
科目:
来源:2012-2013学年云南省昆明一中高三(上)第一次月考数学试卷(文科)(解析版)
题型:填空题
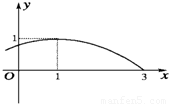
函数f(x)=sin(ωx+ϕ),(x∈R,ω>0,0≤ϕ<2π)的部分图象如图所示,则ω=
ϕ=
.
查看答案和解析>>
科目:
来源:2012-2013学年云南省昆明一中高三(上)第一次月考数学试卷(文科)(解析版)
题型:填空题
已知过点P(1,0)且倾斜角为60°的直线l与抛物线y2=4x交于A,B两点,则弦长|AB|= .
查看答案和解析>>
科目:
来源:2012-2013学年云南省昆明一中高三(上)第一次月考数学试卷(文科)(解析版)
题型:填空题
为估计一圆柱形烧杯A底面积的大小,做以下实验:在一个底面边长为a的正四棱柱容器B中装有一定量的白色小球子,现用烧杯A盛满黑色小珠子(珠子与杯口平齐),将其倒入容器B中,并充分混合,此时容器B中小珠子的深度刚好为a(两种颜色的小珠子大小形状完全相同,且白色的多于黑色的)现从容器B中随机取出100个小珠子,清点得黑色小珠子有25个.若烧杯A的高度为h,于是可估计此烧杯的底面积S约等于 .
查看答案和解析>>
科目:
来源:2012-2013学年云南省昆明一中高三(上)第一次月考数学试卷(文科)(解析版)
题型:填空题
△ABC的内角A、B、C的对边长分别为a、b、c,若a2-c2=b,且b=3ccosA,则b= .
查看答案和解析>>
科目:
来源:2012-2013学年云南省昆明一中高三(上)第一次月考数学试卷(文科)(解析版)
题型:解答题
设公比小于零的等比数列{an}的前n项和为Sn,且a1=-1,S3=3a3.
(I)求数列{an}的通项公式;
(II)若数列{bn}满足bn=an+2n-1,求数列{bn}的前n项Tn.
查看答案和解析>>
科目:
来源:2012-2013学年云南省昆明一中高三(上)第一次月考数学试卷(文科)(解析版)
题型:解答题
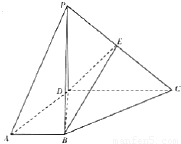
如图,四棱锥P-ABCD的底面为梯形,BA⊥AD,CD⊥AD,PD⊥底面ABCD,PD=AD=AB=1,CD=2AB.E为PC的中点.
(I)证明:EB∥平面PAD;
(II)求证:BC⊥平面PBD;
(II)求四面体P-BDE的体积.
查看答案和解析>>
科目:
来源:2012-2013学年云南省昆明一中高三(上)第一次月考数学试卷(文科)(解析版)
题型:解答题
某高校从参加今年自主招生考试的学生中抽取成绩排名在前80名的学生成绩进行统计,得频率分布表:
| 组号 | 分组 | 频数 | 频率 |
| 1 | [200,210) | 8 | 0.1 |
| 2 | [210,220) | 9 | 0.1125 |
| 3 | [220,230) | ① | |
| 4 | [230,240) | 10 | ② |
| 5 | [240,250) | 15 | 0.1875 |
| 6 | [250,260) | 12 | 0.15 |
| 7 | [260,270) | 8 | 0.10 |
| 8 | [270,280) | 4 | 0.05 |
(I)分别写出表中①、②处的数据;
(II)高校决定在第6、7、8组中用分层抽样的方法选6名学生进行心理测试,最后确定两名
学生给予奖励.规则如下:
若该获奖学生的第6组,给予奖励1千元;
若该获奖学生的第7组,给予奖励2千元;
若该获奖学生的第8组,给予奖励3千元;
测试前,高校假设每位学生通过测试获得奖励的可能性相同.求此次测试高校将要支付的奖金总额为4千元的概率.
查看答案和解析>>





