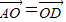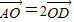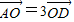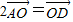相关习题
0 76591 76599 76605 76609 76615 76617 76621 76627 76629 76635 76641 76645 76647 76651 76657 76659 76665 76669 76671 76675 76677 76681 76683 76685 76686 76687 76689 76690 76691 76693 76695 76699 76701 76705 76707 76711 76717 76719 76725 76729 76731 76735 76741 76747 76749 76755 76759 76761 76767 76771 76777 76785 266669
科目:
来源:2012-2013学年四川省成都市高三(上)摸底数学试卷(理科)(解析版)
题型:解答题
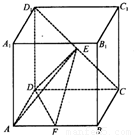
如图,已知正方体ABCD-A
1B
1C
1D
1的棱长为2,E、F分别是D
1C、AB的中点.
(I)求证:EF∥平面ADD
1A
1;
(Ⅱ)求二面角D-EF-A的余弦值.
查看答案和解析>>
科目:
来源:2012-2013学年四川省成都市高三(上)摸底数学试卷(理科)(解析版)
题型:解答题
某幼儿园在“六•一儿童节“开展了一次亲子活动,此次活动由宝宝和父母之一(后面以家长代称)共同完成,幼儿园提供了两种游戏方案:
方案一宝宝和家长同时各抛掷一枚质地均匀的正方体骰子(六个面的点数分别是1,2,3,4,5,6),宝宝所得点数记为x,家长所得点数记为y;
方案二宝宝和家长同时按下自己手中一个计算器的按钮(此计算器只能产生区间[1,6],的随机实数),宝宝的计算器产生的随机实数记为m,家长的计算器产生的随机实数记为挖.
(I)在方案一中,若x+l=2y,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率;
(Ⅱ)在方案二中,若m>2n,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率.
查看答案和解析>>
科目:
来源:2012-2013学年四川省成都市高三(上)摸底数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=logax,g(x)=loga(2x+m-2),其中x∈[1,2],a>0且a≠1,m∈R.
(I)当m=4时,若函数F(x)=f(x)+g(x)有最小值2,求a的值;
(Ⅱ)当0<a<l时,f(x)≥2g(x)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年四川省成都市高三(上)摸底数学试卷(理科)(解析版)
题型:解答题
已知双曲线
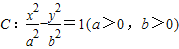
的左、右顶点分别为A、B,右焦点为F(

,0),
一条渐近线的方程为

,点P为双曲线上不同于A、B的任意一点,过P作x轴的垂线交双曲线于另一点Q.
(I)求双曲线C的方程;
(Ⅱ)求直线AP与直线BQ的交点M的轨迹E的方程;
(Ⅲ)过点N(l,0)作直线l与(Ⅱ)中轨迹E交于不同两点R、S,已知点T(2,0),设

的取值范围.

查看答案和解析>>
科目:
来源:2012-2013学年四川省成都市高三(上)摸底数学试卷(理科)(解析版)
题型:解答题
设数列

,数列{b
n}满足:b
n=a
n+1-a
n.
(I)求a
,a
2;
(II)当n∈N
*时,求证:数列{b
n}为等差数列;
(III)设

,求证:

.
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省哈尔滨三中高三(上)10月月考数学试卷(文科)(解析版)
题型:选择题
全集U=R,集合A={x|x2-4≤0},集合B={x|2x-1>1},则A∩B=( )
A.[1,2]
B.(1,2]
C.[1,2)
D.(-∞,2]
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省哈尔滨三中高三(上)10月月考数学试卷(文科)(解析版)
题型:选择题
已知角α是第二象限角,角α的终边经过点P(x,4),且
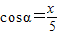
,则tanα=( )
A.

B.

C.
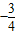
D.
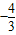
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省哈尔滨三中高三(上)10月月考数学试卷(文科)(解析版)
题型:选择题
已知O是△ABC所在平面内一点,D为BC边中点,且
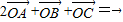
,那么( )
A.
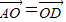
B.
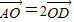
C.
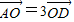
D.
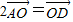
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省哈尔滨三中高三(上)10月月考数学试卷(文科)(解析版)
题型:选择题
已知tanα=-2,则
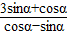
的值为( )
A.

B.

C.
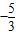
D.-5
查看答案和解析>>
科目:
来源:2012-2013学年黑龙江省哈尔滨三中高三(上)10月月考数学试卷(文科)(解析版)
题型:选择题
已知p:α为第二象限角,q:sinα>cosα,则p是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>


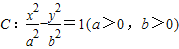 的左、右顶点分别为A、B,右焦点为F(
的左、右顶点分别为A、B,右焦点为F( ,0),
,0), ,点P为双曲线上不同于A、B的任意一点,过P作x轴的垂线交双曲线于另一点Q.
,点P为双曲线上不同于A、B的任意一点,过P作x轴的垂线交双曲线于另一点Q. 的取值范围.
的取值范围.
 ,数列{bn}满足:bn=an+1-an.
,数列{bn}满足:bn=an+1-an. ,求证:
,求证: .
.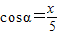 ,则tanα=( )
,则tanα=( )

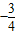
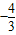
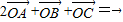 ,那么( )
,那么( )