相关习题
0 76640 76648 76654 76658 76664 76666 76670 76676 76678 76684 76690 76694 76696 76700 76706 76708 76714 76718 76720 76724 76726 76730 76732 76734 76735 76736 76738 76739 76740 76742 76744 76748 76750 76754 76756 76760 76766 76768 76774 76778 76780 76784 76790 76796 76798 76804 76808 76810 76816 76820 76826 76834 266669
科目:
来源:2012-2013学年江苏省常州一中高三(上)第二次练习数学试卷(理科)(解析版)
题型:填空题
已知

是平面内两个互相垂直的单位向量,若向量

满足

,则

最大值是
.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省常州一中高三(上)第二次练习数学试卷(理科)(解析版)
题型:填空题
酒杯的形状为倒立的圆锥,杯深8cm,上口宽6cm,水以20cm3/s的流量倒入杯中,当水深为4cm时,则水面升高的瞬时变化率是 .
查看答案和解析>>
科目:
来源:2012-2013学年江苏省常州一中高三(上)第二次练习数学试卷(理科)(解析版)
题型:填空题
已知函数

,函数

-a+1(a>0),若存在x
1、x
2∈[0,1],使得f(x
1)=g(x
2)成立,则实数a的取值范围是
.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省常州一中高三(上)第二次练习数学试卷(理科)(解析版)
题型:填空题
定义函数f(x)=[x[x]],其中[x]表示不超过x的最大整数,如:[1.5]=1,[-1.3]=-2,当x∈[0,n)(n∈N
*)时,设函数f(x)的值域为A,记集合A中的元素个数为a
n,则式子[
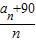
]的最小值为
.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省常州一中高三(上)第二次练习数学试卷(理科)(解析版)
题型:解答题
在平面直角坐标系中,点

在角α的终边上,点Q(sin
2θ,-1)在角β的终边上,且

.
(1)求cos2θ;
(2)求sin(α+β)的值.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省常州一中高三(上)第二次练习数学试卷(理科)(解析版)
题型:解答题
已知命题P:函数
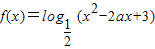
在(-∞,1]内为单调递增函数,命题Q:函数f(x)=x|x-a|+2x在R上单调递增;
(1)若命题Q为真,求实数a的范围;
(2)若p∨q为真,p∧q为假,求实数a的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省常州一中高三(上)第二次练习数学试卷(理科)(解析版)
题型:解答题
设函数

.
(Ⅰ)求f(x)的最大值,并写出使f(x)取最大值是x的集合;
(Ⅱ)已知△ABC中,角A,B,C的对边分别为a,b,c.若

.求a的最小值.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省常州一中高三(上)第二次练习数学试卷(理科)(解析版)
题型:解答题
因客流量临时增大,某鞋店拟用一个高为50cm(即EF=50cm)的平面镜自制一个竖直摆放的简易鞋镜.根据经验,一般顾客AB的眼睛B到地面的距离x(cm)在区间[140,180]内.设支架FG高为h(0<h<90)cm,AG=100cm,顾客可视的镜像范围为CD(如图所示),记CD的长度为y(y=GD-GC).
(1)当h=40cm时,试求y关于x的函数关系式和y的最大值;
(2)当顾客的鞋A在镜中的像A
1满足不等关系GC<GA
1≤GD(不计鞋长)时,称顾客可在镜中看到自己的鞋,若一般顾客都能在镜中看到自己的鞋,试求h的取值范围.

查看答案和解析>>
科目:
来源:2012-2013学年江苏省常州一中高三(上)第二次练习数学试卷(理科)(解析版)
题型:解答题
设函数
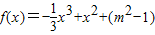
x(x∈R),其中m>0.
(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线的斜率;
(2)求函数f(x)的单调区间与极值;
(3)已知函数f(x)有三个互不相同的零点0,x
1,x
2,且x
1<x
2,若对任意的x∈[x
1,x
2],f(x)>f(1)恒成立,求m的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省常州一中高三(上)第二次练习数学试卷(理科)(解析版)
题型:解答题
已知数列{a
n}满足a
1=1,a
2=-1,当n≥3,n∈N
*时,

.
(1)求数列{a
n}的通项公式;
(2)是否存在k∈N
*,使得n≥k时,不等式S
n+(2λ-1)a
n+8λ≥4对任意实数λ∈[0,1]恒成立?若存在,求出k的最小值;若不存在,请说明理由.
(3)在x轴上是否存在定点A,使得三点

、

、

(其中n、m、k是互不相等的正整数且n>m>k≥2)到定点A的距离相等?若存在,求出点A及正整数n、m、k;若不存在,说明理由.
查看答案和解析>>

 ,函数
,函数 -a+1(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .
-a+1(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .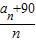 ]的最小值为 .
]的最小值为 . 在角α的终边上,点Q(sin2θ,-1)在角β的终边上,且
在角α的终边上,点Q(sin2θ,-1)在角β的终边上,且 .
.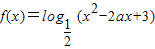 在(-∞,1]内为单调递增函数,命题Q:函数f(x)=x|x-a|+2x在R上单调递增;
在(-∞,1]内为单调递增函数,命题Q:函数f(x)=x|x-a|+2x在R上单调递增; .
. .求a的最小值.
.求a的最小值.
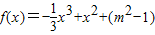 x(x∈R),其中m>0.
x(x∈R),其中m>0. .
. 、
、 、
、 (其中n、m、k是互不相等的正整数且n>m>k≥2)到定点A的距离相等?若存在,求出点A及正整数n、m、k;若不存在,说明理由.
(其中n、m、k是互不相等的正整数且n>m>k≥2)到定点A的距离相等?若存在,求出点A及正整数n、m、k;若不存在,说明理由.