相关习题
0 77029 77037 77043 77047 77053 77055 77059 77065 77067 77073 77079 77083 77085 77089 77095 77097 77103 77107 77109 77113 77115 77119 77121 77123 77124 77125 77127 77128 77129 77131 77133 77137 77139 77143 77145 77149 77155 77157 77163 77167 77169 77173 77179 77185 77187 77193 77197 77199 77205 77209 77215 77223 266669
科目:
来源:2007-2008学年江苏省南通市如东县高二(上)期末数学试卷(解析版)
题型:解答题
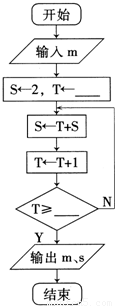
已知数列a
n中,a
1=2,且a
n=n+a
n-1(n≥2),求这个数列的第m项a
m的值(m≥2).现给出此算法流程图的一部分如图.
(Ⅰ)请将空格部分(两个)填上适当的内容;
(Ⅱ)用“For”循环语句写出对应的算法;
(Ⅲ)若输出S=16,则输入的m的值是多少?
查看答案和解析>>
科目:
来源:2007-2008学年江苏省南通市如东县高二(上)期末数学试卷(解析版)
题型:解答题
甲、乙两台机床在相同的技术条件下,同时生产一种零件,现在从中抽测10个,它们的尺寸分别如下(单位:mm).
甲机床:10.2 10.1 10 9.8 9.9
10.3 9.7 10 9.9 10.1;
乙机床:10.3 10.4 9.6 9.9 10.1
10.9 8.9 9.7 10.2 10
(1)用茎叶图表示甲,乙两台机床所生产零件的尺寸;
(2)分别计算上面两个样本的平均数和方差.如果图纸规定零件的尺寸为10mm,从计算的结果来看哪台机床加工这种零件较合适?(要求写出公式,并利用公式笔算)
查看答案和解析>>
科目:
来源:2007-2008学年江苏省南通市如东县高二(上)期末数学试卷(解析版)
题型:解答题
设关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:
来源:2007-2008学年江苏省南通市如东县高二(上)期末数学试卷(解析版)
题型:解答题
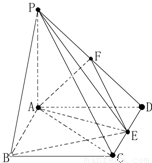
如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=
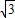
,点F是PD的中点,点E在CD上移动.
(1)求三棱锥E-PAB体积;
(2)求证:PE⊥AF
(3)当点E在CD的什么位置时,EF∥平面PAC,并说明理由.
查看答案和解析>>
科目:
来源:2007-2008学年江苏省南通市如东县高二(上)期末数学试卷(解析版)
题型:解答题
已知α∈[0,π],讨论方程x2cosα+y2sinα=1所表示的曲线的类型,当它表示圆锥曲线时,试求其离心率.
查看答案和解析>>
科目:
来源:2007-2008学年江苏省南通市如东县高二(上)期末数学试卷(解析版)
题型:解答题
椭圆
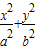
=1(a>b>0)的左右焦点为F
1,F
2,过F
1的直线l与椭圆相交于A,B两点.
(1)若∠AF
1F
2=60°,且点A在以F
1F
2为直径的圆上,求椭圆的离心率;
(2)若a=
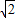
,b=1,求
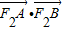
的最大值和最小值.
查看答案和解析>>
科目:
来源:2007-2008学年江苏省南通市如东县高二(上)期末数学试卷(解析版)
题型:解答题
从平面α上取6点,从平面β上取4点,这10个点最多可以确定多少个三棱锥?
查看答案和解析>>
科目:
来源:2007-2008学年江苏省南通市如东县高二(上)期末数学试卷(解析版)
题型:解答题
已知正方体ABCD-A
1B
1C
1D
1的棱长为2,P,Q分别BC,CD上的动点,

,确P,Q的位置,使QB
1⊥PD
1.
查看答案和解析>>
科目:
来源:2007-2008学年江苏省南通市如东县高二(上)期末数学试卷(解析版)
题型:解答题
袋中装有大小相同、质地均匀的3个红球和6个白球,每次从袋中摸出一个球.
(1)一共摸出5个球,求恰好有3个红球的概率;
(2)若有放回的摸球,一共有5次摸球的机会,在摸球过程中,若有三次摸到红球则停止.记停止摸球时,已经摸到红球的次数为ξ,求ξ的概率分布列和数学期望.
查看答案和解析>>
科目:
来源:2007-2008学年江苏省南通市如东县高二(上)期末数学试卷(解析版)
题型:解答题
已知点B(-1,0),C(1,0),P是平面上一动点,且满足

.
(1)求点P的轨迹C对应的方程;
(2)已知点A(m,2)在曲线C上,过点A作曲线C的两条弦AD,AE,且AD,AE的斜率k
1、k
2满足k
1•k
2=2.求证:直线DE过定点,并求出这个定点.
查看答案和解析>>

 已知数列an中,a1=2,且an=n+an-1(n≥2),求这个数列的第m项am的值(m≥2).现给出此算法流程图的一部分如图.
已知数列an中,a1=2,且an=n+an-1(n≥2),求这个数列的第m项am的值(m≥2).现给出此算法流程图的一部分如图.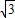 ,点F是PD的中点,点E在CD上移动.
,点F是PD的中点,点E在CD上移动.
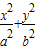 =1(a>b>0)的左右焦点为F1,F2,过F1的直线l与椭圆相交于A,B两点.
=1(a>b>0)的左右焦点为F1,F2,过F1的直线l与椭圆相交于A,B两点.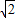 ,b=1,求
,b=1,求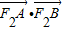 的最大值和最小值.
的最大值和最小值. ,确P,Q的位置,使QB1⊥PD1.
,确P,Q的位置,使QB1⊥PD1. .
.