相关习题
0 77243 77251 77257 77261 77267 77269 77273 77279 77281 77287 77293 77297 77299 77303 77309 77311 77317 77321 77323 77327 77329 77333 77335 77337 77338 77339 77341 77342 77343 77345 77347 77351 77353 77357 77359 77363 77369 77371 77377 77381 77383 77387 77393 77399 77401 77407 77411 77413 77419 77423 77429 77437 266669
科目:
来源:2011-2012学年湖北省襄阳四中、荆州中学、龙泉中学联考高二(下)期中数学试卷(理科)(解析版)
题型:解答题
已知抛物线y
2=4x,过点M(0,2)的直线l与抛物线交于A、B两点,且直线l与x交于点C.
(1)求证:|MA|,|MC|、|MB|成等比数列;
(2)设
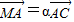
,
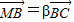
,试问α+β是否为定值,若是,求出此定值;若不是,请说明理由.
查看答案和解析>>
科目:
来源:2011-2012学年湖北省襄阳四中、荆州中学、龙泉中学联考高二(下)期中数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=x
2+2|lnx-1|.
(1)求函数y=f(x)的最小值;
(2)证明:对任意x∈[1,+∞),lnx≥
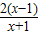
恒成立;
(3)对于函数f(x)图象上的不同两点A(x
1,y
1),B(x
2,y
2)(x
1<x
2),如果在函数f(x)图象上存在点M(x
,y
)(其中x
∈(x
1,x
2))使得点M处的切线l∥AB,则称直线AB存在“伴侣切线”.特别地,当x
=
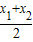
时,又称直线AB存在“中值伴侣切线”.试问:当x≥e时,对于函数f(x)图象上不同两点A、B,直线AB是否存在“中值伴侣切线”?证明你的结论.
查看答案和解析>>
科目:
来源:2013-2014学年浙江省温州市八校联考高三(上)期初数学试卷(文科)(解析版)
题型:选择题
已知全集U={1,2,3,4,5},A={1,2,3},B={3,4,5},则A∩(∁UB)=( )
A.{3}
B.{1,2}
C.{4,5}
D.∅
查看答案和解析>>
科目:
来源:2013-2014学年浙江省温州市八校联考高三(上)期初数学试卷(文科)(解析版)
题型:选择题
已知复数z=i(1-i),(i为虚数单位),则|z|=( )
A.1
B.1+i
C.2
D.
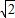
查看答案和解析>>
科目:
来源:2013-2014学年浙江省温州市八校联考高三(上)期初数学试卷(文科)(解析版)
题型:选择题
已知a∈R,则a=0是函数y=x2+ax+1为偶函数的( )
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
查看答案和解析>>
科目:
来源:2013-2014学年浙江省温州市八校联考高三(上)期初数学试卷(文科)(解析版)
题型:选择题
设α,β是两个不同的平面,l是一条直线,以下命题正确的是( )
A.若l⊥α,α⊥β,则l?β
B.若l∥α,α∥β,则l?β
C.若l⊥α,α∥β,则l⊥β
D.若l∥α,α⊥β,则l⊥β
查看答案和解析>>
科目:
来源:2013-2014学年浙江省温州市八校联考高三(上)期初数学试卷(文科)(解析版)
题型:选择题
图为一个几何体的三视国科,尺寸如图所示,则该几何体的体积为( )
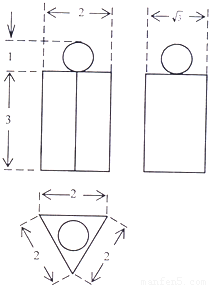
A.
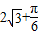
B.
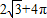
C.

D.
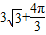
查看答案和解析>>
科目:
来源:2013-2014学年浙江省温州市八校联考高三(上)期初数学试卷(文科)(解析版)
题型:选择题
已知角a的终边与单位圆x
2+y
2=1交于P(

,y),则sin(

+2a)=( )
A.-

B.1
C.

D.-

查看答案和解析>>
科目:
来源:2013-2014学年浙江省温州市八校联考高三(上)期初数学试卷(文科)(解析版)
题型:选择题
已知函数y=f(x)的定义域为R,满足(x-2)f′(x)>0,且函数y=f(x+2)为偶函数,a=f(2),b=f(log
23),c=f(
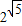
),则实数a,b,c的大小关系是( )
A.a>b>c
B.c>b>a
C.b>c>a
D.c>a>b
查看答案和解析>>
科目:
来源:2013-2014学年浙江省温州市八校联考高三(上)期初数学试卷(文科)(解析版)
题型:选择题
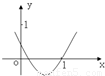
如图是二次函数f(x)=x
2-bx+a的部分图象,则函数g(x)=e
x+f′(x)的零点所在的区间是( )
A.(-1,0)
B.(0,1)
C.(1,2)
D.(2,3)
查看答案和解析>>

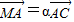 ,
,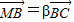 ,试问α+β是否为定值,若是,求出此定值;若不是,请说明理由.
,试问α+β是否为定值,若是,求出此定值;若不是,请说明理由.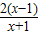 恒成立;
恒成立;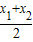 时,又称直线AB存在“中值伴侣切线”.试问:当x≥e时,对于函数f(x)图象上不同两点A、B,直线AB是否存在“中值伴侣切线”?证明你的结论.
时,又称直线AB存在“中值伴侣切线”.试问:当x≥e时,对于函数f(x)图象上不同两点A、B,直线AB是否存在“中值伴侣切线”?证明你的结论.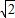

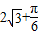
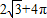

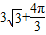
 ,y),则sin(
,y),则sin( +2a)=( )
+2a)=( )


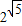 ),则实数a,b,c的大小关系是( )
),则实数a,b,c的大小关系是( )