相关习题
0 77445 77453 77459 77463 77469 77471 77475 77481 77483 77489 77495 77499 77501 77505 77511 77513 77519 77523 77525 77529 77531 77535 77537 77539 77540 77541 77543 77544 77545 77547 77549 77553 77555 77559 77561 77565 77571 77573 77579 77583 77585 77589 77595 77601 77603 77609 77613 77615 77621 77625 77631 77639 266669
科目:
来源:2012-2013年广东省汕头市东厦中学高三(上)第三次质检数学试卷(理科)(解析版)
题型:填空题
查看答案和解析>>
科目:
来源:2012-2013年广东省汕头市东厦中学高三(上)第三次质检数学试卷(理科)(解析版)
题型:填空题
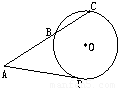
如图,已知圆O的半径为2,从圆O外一点A引切线AD和割线ABC,圆心O到AC的距离为
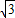
,AB=3,则切线AD的长为
.
查看答案和解析>>
科目:
来源:2012-2013年广东省汕头市东厦中学高三(上)第三次质检数学试卷(理科)(解析版)
题型:解答题
一盒中装有20个大小相同的弹子球,其中红球10个,白球6个,黄球4个,一小孩随手拿出4个,求至少有3个红球的概率.
查看答案和解析>>
科目:
来源:2012-2013年广东省汕头市东厦中学高三(上)第三次质检数学试卷(理科)(解析版)
题型:解答题
查看答案和解析>>
科目:
来源:2012-2013年广东省汕头市东厦中学高三(上)第三次质检数学试卷(理科)(解析版)
题型:解答题
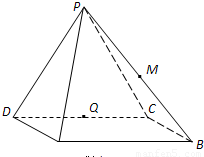
四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是∠ADC=60°的菱形,M为PB的中点,Q为CD的中点.
(1)求证:PA⊥CD;
(2)求AQ与平面CDM所成的角.
查看答案和解析>>
科目:
来源:2012-2013年广东省汕头市东厦中学高三(上)第三次质检数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=x
4+ax
3+2x
2+b(x∈R),其中a,b∈R.
(Ⅰ)当
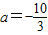
时,讨论函数f(x)的单调性;
(Ⅱ)若函数f(x)仅在x=0处有极值,求a的取值范围;
(Ⅲ)若对于任意的a∈[-2,2],不等式f(x)≤1在[-1,1]上恒成立,求b的取值范围.
查看答案和解析>>
科目:
来源:2012-2013年广东省汕头市东厦中学高三(上)第三次质检数学试卷(理科)(解析版)
题型:解答题
据调查,湖南某地区有100万从事传统农业的农民,人均年收入3000元.为了增加农民的收入,当地政府积极引资建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作.据估计,如果有x(x>0)万人进入企业工作,那么剩下从事传统农业的农民的人均年收入有望提高2x%,而进入企业工作的农民人均年收入为3000a元(a>0为常数).
(I)在建立加工企业后,要使该地区从事传统农业的农民的年总收入不低于加工企业建立前的年总收入,求x的取值范围;
(Ⅱ)在(I)的条件下,当地政府应安排多少万农民进入加工企业工作,才能使这100万农民的人均年收入达到最大?
查看答案和解析>>
科目:
来源:2012-2013年广东省汕头市东厦中学高三(上)第三次质检数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=ax
2+bx+1(a,b为实数),x∈R,
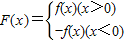
(1)若f(-1)=0,且函数f(x)的值域为[0,+∞),求F(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(3)设m>0,n<0,m+n>0,a>0且f(x)为偶函数,判断F(m)+F(n)能否大于零?
查看答案和解析>>
科目:
来源:2012-2013学年河北省保定市高二(下)期中数学试卷(理科)(解析版)
题型:选择题
复数
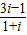
(i为虚数单位)的模是( )
A.
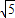
B.
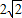
C.5
D.8
查看答案和解析>>
科目:
来源:2012-2013学年河北省保定市高二(下)期中数学试卷(理科)(解析版)
题型:选择题
在极坐标系中,已知点P(2,
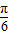
),则过点P且平行于极轴的直线的方程是( )
A.ρsinθ=1
B.ρsinθ=
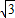
C.ρcosθ=1
D.ρcosθ=
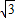
查看答案和解析>>

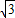 ,AB=3,则切线AD的长为 .
,AB=3,则切线AD的长为 .

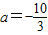 时,讨论函数f(x)的单调性;
时,讨论函数f(x)的单调性;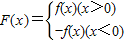
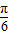 ),则过点P且平行于极轴的直线的方程是( )
),则过点P且平行于极轴的直线的方程是( )