相关习题
0 77542 77550 77556 77560 77566 77568 77572 77578 77580 77586 77592 77596 77598 77602 77608 77610 77616 77620 77622 77626 77628 77632 77634 77636 77637 77638 77640 77641 77642 77644 77646 77650 77652 77656 77658 77662 77668 77670 77676 77680 77682 77686 77692 77698 77700 77706 77710 77712 77718 77722 77728 77736 266669
科目:
来源:2013-2014学年安徽省安庆市望江四中高三(上)第一次月考数学试卷(文科)(解析版)
题型:选择题
函数f(x)=lnx+2x-6的零点所在的区间为( )
A.(1,2)
B.(

,2)
C.(2,

)
D.(

,3)
查看答案和解析>>
科目:
来源:2013-2014学年安徽省安庆市望江四中高三(上)第一次月考数学试卷(文科)(解析版)
题型:选择题
设集合M是R的子集,如果点x
∈R满足:?a>0,?x∈M,0<|x-x
|<a,称x
为集合M的聚点.则下列集合中以1为聚点的有( )
①
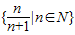
;
②

;
③Z;
④{y|y=2
x}.
A.①④
B.②③
C.①②
D.①②④
查看答案和解析>>
科目:
来源:2013-2014学年安徽省安庆市望江四中高三(上)第一次月考数学试卷(文科)(解析版)
题型:选择题
一个盒子里有3个分别标有号码为1,2,3的小球,每次取出一个,记下它的标号后再放回盒子中,共取3次,则取得小球标号最大值是3的取法有( )
A.12种
B.15种
C.17种
D.19种
查看答案和解析>>
科目:
来源:2013-2014学年安徽省安庆市望江四中高三(上)第一次月考数学试卷(文科)(解析版)
题型:选择题
已知函数f(x)=a•2
|x|+1(a≠0),定义函数

给出下列命题:
①F(x)=|f(x)|;
②函数F(x)是奇函数;
③当a<0时,若mn<0,m+n>0,总有F(m)+F(n)<0成立,
其中所有正确命题的序号是( )
A.②
B.①③
C.②③
D.①②
查看答案和解析>>
科目:
来源:2013-2014学年安徽省安庆市望江四中高三(上)第一次月考数学试卷(文科)(解析版)
题型:填空题
函数

的定义域为
.
查看答案和解析>>
科目:
来源:2013-2014学年安徽省安庆市望江四中高三(上)第一次月考数学试卷(文科)(解析版)
题型:填空题
数列{a
n}的通项公式a
n=ncos

,其前n项和为S
n,则S
2013=
.
查看答案和解析>>
科目:
来源:2013-2014学年安徽省安庆市望江四中高三(上)第一次月考数学试卷(文科)(解析版)
题型:填空题
连掷两次骰子得到的点数分别为m和n,若记向量

=(m,n)与向量

的夹角为θ,则θ为锐角的概率是
.
查看答案和解析>>
科目:
来源:2013-2014学年安徽省安庆市望江四中高三(上)第一次月考数学试卷(文科)(解析版)
题型:填空题
函数y=log2(x2-ax+2)在[2,+∞)上恒为正,则实数a的取值范围是 .
查看答案和解析>>
科目:
来源:2013-2014学年安徽省安庆市望江四中高三(上)第一次月考数学试卷(文科)(解析版)
题型:填空题
定义在(-∞,0)∪(0,+8)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“等比函数”.现有定义在(-∞,0)∪(0,+∞上的如下函数:
①f(x)=2x;
②f(x)=log2|x|;
③f(x)=x2;
④f(x)=ln2x,
则其中是“等比函数”的f(x)的序号为 .
查看答案和解析>>
科目:
来源:2013-2014学年安徽省安庆市望江四中高三(上)第一次月考数学试卷(文科)(解析版)
题型:解答题
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
(1)sin213°+cos217°-sin13°cos17°
(2)sin215°+cos215°-sin15°cos15°
(3)sin218°+cos212°-sin18°cos12°
(4)sin2(-18°)+cos248°-sin2(-18°)cos48°
(5)sin2(-25°)+cos255°-sin2(-25°)cos55°
(Ⅰ)试从上述五个式子中选择一个,求出这个常数
(Ⅱ)根据(Ⅰ)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
查看答案和解析>>

 ,2)
,2) )
) ,3)
,3)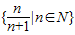 ;
;  ;
;  给出下列命题:
给出下列命题: ,其前n项和为Sn,则S2013= .
,其前n项和为Sn,则S2013= . =(m,n)与向量
=(m,n)与向量 的夹角为θ,则θ为锐角的概率是 .
的夹角为θ,则θ为锐角的概率是 .